Mathematicianadda

Perimeter of Rectangle

from Math Blog http://bit.ly/2Ifqg5P

Prove that the Length of the Latus Rectum of the Hyperbola

from Math Blog http://bit.ly/2HO7Tpu

Finding Center Foci Vertices and Directrix of Ellipse and Hyperbola

from Math Blog http://bit.ly/2MhVQF4

submitted by /u/AutoModerator
[link] [comments]

from math http://bit.ly/2W7FEFX

I do have views about open access, and you might have expected me to discuss Plan S before now. But I know quite a bit more about it than I did, thanks to two things: a visit to the department by our very helpful open access staff from the Library, and a list of FAQs from Scholastica, the back-end organisation behind beautiful open-access journals such as Discrete Analysis.

A universe in which Plan S was fully implemented would have some advantages over the present one, as I hope will become apparent below. But revolutions are always messy, and this one seems likely to be no exception. Although the start date is supposed to be January 2020, there is a great deal yet which has not been agreed; it is rumoured that the group behind Plan S have rowed back from some of their more extreme positions (but also that this was done partly because of pressure from the major academic publishers, who are keen not to lose the huge profits they make on the back of our labours).

Plan S mandates that all funders of research who sign up to it will require the results of the research to be published open-access. So far, so uncontroversial. But there is more to it. Very many journals now are “hybrid”, so that you can choose to pay article processing charges (APCs) and have your paper published open-access, or not, in which case it is available to subscribers only (perhaps for some limited period). One thing which Plan S will implement, it seems, is that hybrid journals will no longer be tolerated; publicly funded research must appear in journals which are fully open access. (Why?)

There are various issues here:

• Learned societies often get the bulk of their income from publishing activities. It is quite possible that a move to APCs will severely dent this income. The rules are not drawn up with learned societies in mind, and no provision has been made to mitigate the blow.
• Governments in some countries provide universities with money to pay APCs for open access publication. But this raises problems of its own. First, there are authors who have no affiliation with a university, and as I understand it there is no provision for them (apart from a vague commitment to support Third World academics). Second, if an institution doesn’t have enough money to pay for all its researchers’ publications, someone (probably not an academic) has to decide who gets to publish and who doesn’t.
• Plan S will set an acceptable level of APCs. I have not found anywhere any indication of what this will be. At present, commercial publishers charge several thousand euros per paper. Nothing I read in the Plan S documents suggests that this is regarded as much too high.

On the face of it, it takes away researchers’ freedom to choose where to publish, since the number of Plan S-compliant journals is likely to be small (at least in the early stages). In some subjects more than others, young researchers feel that the journals in which they publish have a big effect on their subsequent careers.

However, leaving that aside, Scholastica are naturally more interested in how to ensure that your journal is Plan S-compliant. You might think that a pure diamond open access journal, like the one I am proud to be associated with, would not have any difficulty. But, as I said, the rules were designed under pressure from large publishers, and this assumption is by no means true.

To be Plan S-compliant, a journal must satisfy the following conditions (and others):

• The journal must be fully open-access, with copyright held by the authors under a CC-BY licence. (Scholastica point out that they have just introduced a scheme for journal editors to set a default copyright licence.)
• It must have no or low APCs (see above).
• It must be registered in the Directory of Open Access Journals.
• Articles must have DOIs.
• Articles must be archived in an official repository.
• Where possible, articles and data must be in formats (such as XML) which are fully machine-searchable. This applies also to article metadata. (Fine for metadata, but until we have XML that can produce the quality of typesetting we get from LaTeX, mathematicians are unlikely to be happy with the first requirement.)

In other words, things that would be useful if they existed, which the big publishers already provide (mostly), and which will be troubling to implement for small publishers.

It should also be noted that Plan S will permit “transitional arrangements” to be negotiated. But it is expected that large publishers will have the resources for these, which tend to apply at national level (indeed Springer already have such arrangements in place), whereas again small publishers will struggle.

You might think that this is just a European issue, but it is not. Already the Bill and Melinda Gates Foundation has signed up, and Plan S is actively seeking further support. Also, you might think that, if you don’t have a public research grant, you will be immune; but think about possible coauthors (who might be students or postdocs, or work in a country where university staff are government employees). It is not an exaggeration to say that this affects all of us.

from Peter Cameron's Blog http://bit.ly/2MmzDFV

In the below diagram, A, B, C, D, E, F are beaver lodges and the segments in blue and red are burrows that connect the lodges. The dots marked with the letters G to S are crossing points where the beavers can change track. In the lodge A there are 3 beavers who want to reach their lodges in B, C and D. Obviously each beaver can follow several alternative paths to reach its lodge. According to the number of different paths that each beaver can follow, we will reward each with a corresponding number of apples. Each path consists of several burrows between the crossing points (the lodges in A to F can also be crossing points). A beaver can choose a specific burrow only if its ending crossing point is closer to its destination lodge, with respect to its point of origin. How many apples will each beaver gain?Lodges and burrows

It's really confusing; I can hardly understand the terms. Can anyone help?

For example, from A to B I think it is AB, AOB, ANOB, AOPB, ANOPB.

from Hot Weekly Questions - Mathematics Stack Exchange

Suppose we are given a vector $v$ and vectors $\mu_i$:

$v = \mu_1+\mu_2+...+\mu_m$, where $\mu_i \in R^n$, all $\mu_i$ are of unit length.

Oracle will give me $k$ vectors $\mu_{j_1}, \mu_{j_2},...\mu_{j_k}$ from the original set such that when I project $v$ onto subspace spanned by these vectors the length of the projection is highest possible. In other words, from the set of all combinations of $k$ vectors from $[\mu_1,...\mu_n]$ the $[\mu_{j_1}, \mu_{j_2},...\mu_{j_k}]$ give highest length of projection. Lets denote by $v_{\text{proj}}$ projection of $v$ onto $[\mu_{j_1}, \mu_{j_2},...\mu_{j_k}]$

I want to estimate quality of projection before oracle gives me this $k$ vectors. I want to give upper bound on $||v - v_{\text{proj}}|| $

As far as I understood it is very difficult to obtain these $k$ vectors by myself. However, I know that for any two vectors $\mu_i, \mu_j$, $||\mu_i-\mu_j|| \leq \alpha$, where $\alpha$ is a given positive number.

Small values of $\alpha$ will tell me that all $\mu_i$ are close to each other and heading towards same direction. I would suspect then that projection will be good, and its length will be close to the length of original vector. How can I use this to give an upper bound $||v - v_{\text{proj}}|| $?

My attempts:

Without loss of generality lets assume that $k$ optimal vectors are first $k$ vectors in the list, i.e $\mu_1,\mu_2,...\mu_k$. Lets denote by $P$ projection operator on the space spanned by $\mu_1,\mu_2,...\mu_k$.

$\|v - v_{\text{proj}}\| = \|v - P(v)\| = \|v - P(\mu_1+\mu_2+...+\mu_m)\| = $

$\|v - P(\mu_1) - P(\mu_2) - ... - P(\mu_m)\| = $

$ \| v - \mu_1 - \mu_2 - ... - \mu_k - P(\mu_{k+1}) - P(\mu_{k+2}) - ... - P(\mu_m)\| = $

$\|\mu_{k+1} - P(\mu_{k+1}) + \mu_{k+2} - P(\mu_{k+2}) + ... + \mu_{m} - P(\mu_{m})\|$

$\|v - v_{\text{proj}}\| \leq \|\mu_{k+1} - P(\mu_{k+1})\| + \|\mu_{k+2} - P(\mu_{k+2}) + ... + \|\mu_{m} - P(\mu_{m})\|$

$\|v - v_{\text{proj}}\| \leq (m-k)\alpha$

So in order to make $\|v - v_{\text{proj}}\| \leq \epsilon$, we need $k \geq \frac{m\alpha - \epsilon}{\alpha}$

I am not satisfied with this result because $k$ grows linearly with $m$. I want it to grow much slower, something like $\log(m)$. My goal is to show that under some constraints on $\mu_i$, we need only approximately $\log(m)$ vectors to approximate $v$.

I think the bound can be improved substantially. First Cauchy inequality isn't very tight and second, I used $|\mu_{k+1} - P(\mu_{k+1})\| \leq \alpha$ which is also very loose.

I am open for additional constraints on $\mu_1,...\mu_m$ to achieve logarithmic growth

As Alex Ravsky has noted, we also need a constraint on $\alpha$ in order to achieve logarithmic growth. Assume that $k$ $\leq n$, $\mu_i$ is th $i$-th standard ort of the space $\mathbb{R}^n$, and $\alpha = \sqrt{2}$. Then $\|v - v_{\text{proj}}\| = \sqrt{m-k}$

from Hot Weekly Questions - Mathematics Stack Exchange

Perimeter and Area of Square Worksheet

from Math Blog http://bit.ly/2WlNX6p

Find Vertex Focus Directrix and Latus Rectum of Parabola

from Math Blog http://bit.ly/2I8zhgS

Many of you have probably already heard the news that Tuna Altınel, a mathematician of Turkish nationality working in France, was arrested on a family visit to Turkey. His alleged crimes are signing a petition requesting peace talks, and taking part in a public meeting in Lyon “displeasing to the Turkish government”.

You can find latest news here. This website also explains what you can do to help.

Please do anything you can to call for his immediate release.

from Peter Cameron's Blog http://bit.ly/2WAnelB

Perimeter and Area of Square

from Math Blog http://bit.ly/2wuhUBF

Earlier this month, Anna announced on Twitter “It’s finally happened, I got tapped to teach History of Math. Since I cover so much of the euro white guy stuff in number theory, I want to do a People’s History of … Continue reading →

from Blog on math blogs http://bit.ly/2JP8VUw

submitted by /u/fsbishop
[link] [comments]

from math http://bit.ly/2Kb7a3g

submitted by /u/The_Necromancer10
[link] [comments]

from math http://bit.ly/2wvUE6e

In my capstone class for future secondary math teachers, I ask my students to come up with ideas for engaging their students with different topics in the secondary mathematics curriculum. In other words, the point of the assignment was not to devise a full-blown lesson plan on this topic. Instead, I asked my students to […]

from Mean Green Math

This question is Q.13 of International Mathematical Olympiad Preliminary Selection Contest - Hong Kong 2019.

$A$, $B$, $C$ are three points on a circle while $P$ and $Q$ are two points on $AB$. The extensions of $CP$ and $CQ$ meet the circle at $S$ and $T$ respectively. If $AP=2$, $AQ=7$, $AB=11$, $AS=5$ and $BT=2$, find the length of $ST$.

My approach:

Let $BC=y$ and $AC=z$. It can be found that $CP=\dfrac{2y}5$, $PS=\dfrac{45}y$, $CQ=2z$ and $QT=\dfrac{14}z$. By applying cosine formula on $\triangle BCQ$, $\triangle BCT$, $\triangle ACP$ and $\triangle ACS$, I know that $y^2=\dfrac{1620}{11}$ and $z^2=\dfrac{994}{55}$.

Then I can find $\cos\angle PCQ$ and hence deduce that $ST=\dfrac{25}4$.

The calculation is tedious and I am quite sure that I have missed something. Does anybody have a better method?

from Hot Weekly Questions - Mathematics Stack Exchange

Find the Equation of the Hyperbola with the Given Information

from Math Blog http://bit.ly/2W3X5aq

Alice and Bob are playing a game in which they take turns modifying a $k$-tuple $(t_1,\ldots,t_k)$ of positive integers. Alice plays first. On each turn, a player subtracts a positive multiple of $t_i$ from $t_j$ for some $i\neq j$, subject to the condition that the resulting $k$-tuple consists of positive integers. A player loses if they have no valid moves.

For a given positive integer $k$ and $k$-tuple $(t_1,\ldots,t_k)$ of positive integers, who has a winning strategy and what is it?

---

I have a solution for the $k=2$ case, which I will include here. Let $\phi=\frac{\sqrt{5}+1}{2}$ be the golden ratio. Observe that $\phi$ is irrational, and $\frac{1}{\phi}=\phi-1$.

Clearly the order of the entries in a $k$-tuple does not affect who has a winning strategy. We will order all 2-tuples (pairs) of positive integers $(a,b)$ so that $a\geq b$.

Claim: Alice has a winning strategy for the pair $(a,b)$, where $a\geq b$ are positive integers, if and only if $\frac{a}{b}>\phi$.

Proof: It suffices to show the following for positive integers $a\geq b$.

a) If $\frac{a}{b}>\phi$, then there exists a valid move $(a,b)\to (a',b')$ with $a'\leq b'$ and $\frac{a'}{b'}<\phi$.

b) If $\frac{a}{b}<\phi$, then all valid moves $(a,b)\to (a',b')$ with $a'\geq b'$ satisfy $\frac{a'}{b'}>\phi$.

We first prove b). If $a=b$ then there are no valid moves. If $a>b$ and $\frac{a}{b}<\phi$, then $b<a<\phi b<2b$. Hence there is exactly one valid move, namely $(a,b)\to(b,a-b)$. Clearly $a-b<b$, and $\frac{a-b}{b}=\frac{a}{b}-1<\phi-1=\frac{1}{\phi}$, hence $\frac{b}{a-b}>\phi$ as required.

We now prove a). Let $a,b$ be positive integers with $\frac{a}{b}>\phi$. Write $a=qb+r$ for integers $q,r$, where $0\leq r<b$. Consider the following move $$(a,b)\to\begin{cases} (b,r) & \text{if } b<\phi r, \\ (b+r,b) & \text{otherwise.} \end{cases}$$

The first move is obtained by subtracting $qb$ from $a$, while the second is obtained by subtracting $(q-1)b$ from $a$. In both cases, the resulting pair consists of positive integers. To show this is a valid move, we must show that we are subtracting a positive integer multiple of $b$ from $a$. Since $a>b$, the integer $q$ is positive. If $r=0$, then $a\geq 2b$, hence $q-1$ is positive. If $r\neq0$ and $b>\phi r$, then

$$a-r>b\phi-\frac{b}{\phi}=b,$$

hence $a-r\geq 2b$, so $q-1$ is positive. Thus the described move is valid.

Observe now that if $b<\phi r$ then $\frac{b}{r}<\phi$, as required. If $b>\phi r$, then

$$\frac{b+r}{b}=1+\frac{r}{b}<1+\frac{1}{\phi}=\phi,$$ as required. $\square$

from Hot Weekly Questions - Mathematics Stack Exchange

Find the Equation of the Ellipse with the Given Information

from Math Blog http://bit.ly/2YZwn4U

Find the Equation of the Parabola with the Given Information

from Math Blog http://bit.ly/2VYOrdu

I have been attempting to evaluate this integral and by using wolfram alpha I know that the value is$$I=-\int_0^1 \ln(1+x)\ln(1-x)dx=\frac{\pi^2}{6}+2\ln(2)-\ln^2(2)-2$$

My Attempt:

I start off by parametizing the integral as $$I(a)=\int_0^1 -\ln(1+x)\ln(1-ax)dx$$ where $I=I(1)$. I then differentiate to get $$I'(a)=\int_0^1 \frac{ax\ln(1+x)}{1-ax}dx=\int_0^1 ax\ln(1+x)\sum_{n=0}^\infty(ax)^ndx=\sum_{n=1}^\infty a^{n+1}\int_0^1 x^{n+1}\ln(1+x)dx$$

Evaluating this integral by integration by parts and geometric series I get $$\int_0^1 x^{n+1}\ln(1+x)dx=\frac{x^{n+2}}{n+2}\ln(1+x)|_0^1-\frac{1}{n+2}\int_0^1 \frac{x^{n+2}}{1+x}dx=\frac{\ln(2)}{n+2}-\frac{1}{n+2}\int_0^1 x^{n+2}\sum_{k=0}^\infty(-x)^kdx=\frac{\ln(2)}{n+2}-\frac{1}{n+2}\sum_{k=0}^\infty(-1)^k\int_0^1 x^{k+n+2}dx=\frac{\ln(2)}{n+2}-\frac{1}{n+2}\sum_{k=0}^\infty\frac{(-1)^k}{k+n+2}=\frac{\ln(2)}{n+2}-\frac{1}{2(n+2)}\left(\psi_0\left(\frac{n}{2}+2\right)-\psi_0\left(\frac{n}{2}+\frac{3}{2}\right)\right)$$ So I arrive at $$I'(a)=\sum_{n=0}^\infty a^{n+1}\left(\frac{\ln(2)}{n+2}-\frac{1}{2(n+2)}\left(\psi_0\left(\frac{n}{2}+2\right)-\psi_0\left(\frac{n}{2}+\frac{3}{2}\right)\right)\right)$$ Re-indexing I get $$I'(a)=\frac{\ln(2)}{a}\sum_{n=2}^\infty \frac{a^n}{n}+\frac{1}{2}\sum_{n=2}^\infty \frac{\psi_0\left(\frac{n+1}{2}\right)}{n}a^{n-1}-\frac{1}{2}\sum_{n=2}^\infty \frac{\psi_0\left(\frac{n}{2}+1\right)}{n}a^{n-1}$$Integrating both sides from $0$ to $1$ I recover $I(1)$ $$I(1)=\int_0^1 \frac{\ln(2)}{a}\left(-\ln(1-a)-a\right)da+\frac{1}{2}\sum_{n=2}^\infty \frac{\psi_0\left(\frac{n+1}{2}\right)}{n^2}-\frac{1}{2}\sum_{n=2}^\infty \frac{\psi_0\left(\frac{n}{2}+1\right)}{n^2}$$ Then using the integral equation for the Dilogarithm I arrive at $$I(1)=\ln(2)\int_0^1 -\frac{\ln(1-a)}{a}da-\ln(2)+\frac{1}{2}\sum_{n=2}^\infty \frac{\psi_0\left(\frac{n+1}{2}\right)}{n^2}-\frac{1}{2}\sum_{n=2}^\infty \frac{\psi_0\left(\frac{n}{2}+1\right)}{n^2}$$ $$I(1)=\frac{\ln(2)\pi^2}{6}-\ln(2)+\frac{1}{2}\sum_{n=2}^\infty \frac{\psi_0\left(\frac{n+1}{2}\right)}{n^2}-\frac{1}{2}\sum_{n=2}^\infty \frac{\psi_0\left(\frac{n}{2}+1\right)}{n^2}$$

At this point I could not continue further as I did not know how to simplify the Digamma terms in the sums. I think that by using the Digamma function's relation to the Harmonic Numbers it could be possible to exploit known values of Harmonic sums to arrive at the answer but I could not get the sums in a form where this would work. If anyone could help me continue further or let me know if I am on the right track I would greatly appreciate it. Thank you in advance.

from Hot Weekly Questions - Mathematics Stack Exchange

Practice Questions on Finding Equation of Circle for Grade 12

from Math Blog http://bit.ly/2XiRu1x

How to Check if a Given Point Lies Inside or Outside a Circle

from Math Blog http://bit.ly/30WckpF

submitted by /u/The_Necromancer10
[link] [comments]

from math http://bit.ly/2XbBy13

submitted by /u/1XCSX1
[link] [comments]

from math http://bit.ly/2YYzREy

Equation of Tangents to a Circle Examples

from Math Blog http://bit.ly/2QCihTP

submitted by /u/MrCheapCheap
[link] [comments]

from math http://bit.ly/2KjK8HD

     Sometimes we find that words presented as prose are poetic . . . as these words of British philosopher and mathematician Bertrand Russell (1872-1970):

          At the age of eleven, I began Euclid, 
          with my brother as my tutor. This was one 
          of the great events of my life, as dazzling 
          as first love. I had not imagined 
          that there was anything so delicious in the world.


More thoughtful quotes from Russell may be found here.


from Intersections -- Poetry with Mathematics

29 May 2019

In this Newsletter:

1. New on IntMath: Logarithm function from its graph
2. Breakthrough Junior Challenge
2. Resources: Wolfram, MathGraph32
3. Math in the news: Computers and equations
4. Math movies: Calculus, Probability
5. Math puzzle: Bowling
6. Final thought: extinctions

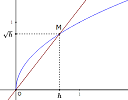
1. New on IntMath: Finding the logarithm function from its graph

This article explains how to observe the characteristics of a logarithmic graph to determine its equation. See: How to find the equation of a logarithm function from its graph?

2. Breakthrough Junior Challenge

One of the best ways to learn something is to explain it to someone else.

The Breakthrough Junior Challenge encourages students to create a short explanatory video. Prizes include a $250,000 post-secondary/college scholarship.

The overall idea, from the site:

Explain a big scientific idea in Physics, Life Sciences or Mathematics with a short video. You will have until June 15, 2019 at 11:59 PM PDT to submit your video (3:00 minutes max).

See these previous prize-winning videos made by students.

The number of submissions for math topics is quite low compared to the other categories. So, give it a go!

3. Resources

(a) Wolfram Language Webinars

Wolfram has released a new version of the Wolfram Language and Mathematica, and is offering 4 free Webinars to explain the new features.

I'm particularly looking forward to the June 12 one, which will cover:

Mathematics and Scientific Visualization
Calculus • Algebra • Complex Visualization • Geographic Visualization • Molecular Visualization

You can register here.

Of course, their main aim is commercial, but you can still learn a lot of worthwhile things by seeing how the experts make use of a powerful mathemtaical tool.

You may also be interested in Wolfram U, a series of videos which explores a range of math topics using Mathematica.

(b) MathGraph 32 - updated to javascript

I've featured MathGraph32 a few times before on IntMath. It's a cross-platform, cross-browser interactive graphing solution, with some very nice features. It's similar in many ways to GeoGebra, but I find it easier to use for many cases.

From the developer, Yves Biton:

"I have entirely rewritten MathGraph32 in JavaScript. It is still free under GNU GPL license. So no more use of Java, a new user interface without menu and new functionalities. Hope it will be useful because it was a tough job!"

MathGraph32 can be used:

1. Online (with easy to use menu icons); or
2. As a stand alone application (download page)

It also works on mobile devices.

Check out these tutorial videos in English, and here are some graph interactives.

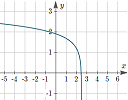
4. Math in the news:

(a) Using computers to crack open centuries-old mathematical puzzles

Throughout history, a lot of mathematical research ended up in the "too hard" basket, because it was just impossible to do all the calculations necessary to draw a conclusion.

One such example is that of Diophantine Equations, the most famous of which was xⁿ + yⁿ = zⁿ, which has no whole number solutions when n is greater than 2, finally proved by Andrew Wiles after 300 years.

Diophantus of Alexandria was a 3rd century BCE Greek mathematician, often called the "father of algebra", as a result of his books on algebraic equations, called Arithmetica, a snippet of which is shown here.

The article Using computers to crack open centuries-old mathematical puzzles by Christopher Rasmussen, Associate Professor of Mathematics at Wesleyan University, explains in layman's language what the researchers aimed to do by using computers.

The actual paper talks about how they used Sagemath, an open-source computer algebra system, to solve cubic Ramanujan-Nagell equations, for example:

x³ + 3^k = qⁿ, where q is an odd prime.

One such solution is x = 2, k = 4, q = 89 and n = 1, giving:

2³ + 3⁴ = 89¹

(b) New memristor circuit solves linear equations in nanoseconds

An example of a simple linear equation written in matrix form is:

(See Matrices and Linear Equations for background.)

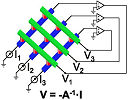A new circuit can solve large cases of such a system of linear equations in a single operation within a few tens of nanoseconds, much faster than using current or quantum methods.

It uses an analog method of in-memory computing, where one equation coefficient is stored as a unique resistance in one memristor (an electrical component that regulates the flow of current in a circuit and remembers the amount of charge that has previously flowed through it, retaining this memory even without power.)

The circuit was tested on a wide set of algebraic problems including:

1. Ranking of internet websites
2. Complex differential equations
3. Finding wave-function of an electron

See: Speeding up artificial intelligence

5. Math Movies

(a) Essence of Calculus - 3Blue1Brown

I've featured 3Blue1Brown's brilliant videos in earlier Newsletters. This time it's the series, Essence of Calculus.

If you are about to embark on studying calculus, this would be a great introduction: See: Essence of Calculus (playlist)

(b) False positive riddle

Mining unobtainium is hard work – the rare mineral appears in only 1% of rocks in the mine. But your friend Tricky Joe has something up his sleeve (involving conditional probability). See: Can you solve the false positive riddle?

6. Math puzzles

The puzzle in the last IntMath Newsletter asked about a general formula for a given sequence. There were an interesting range of responses.

Correct answers with sufficient reasons were submitted by Michael (who used modulus arithmetic) and Russell. Correct solutions (but with missing reasoning or details) were presented by: Gayathri, Christopher, Larry, Arun, and Nicola (who used a recursive approach).

New math puzzle: Bowling

In his latest bowling game, Raj scored 199 and this raised his average over a number of games from 177 to 178. What must he score in the next game to raise his average to 179?

You can leave your response here. Hint: If you present your answer with full explanation of how you obtained it, then others can follow your thinking and learn something from it.

7. Final thought - extinctions

Some years ago I was on a retreat in Malaysia. I enjoy going for walks in the early morning, and one day I followed a track into the (secondary) jungle. I was quite surprised to come across recent evidence (just hours old) of elephants using the same track. It could have been dangerous had I met those elephants, but I was excited to know wild elephants were still in the area. (Most of the virgin jungle in that area has been cleared for palm oil production, so it was doubly surprising.)

So I was saddened by the death this week of the last captive male Sumatran rhino in Malaysia, the last in a country that used to have plenty of them.

There is a real insanity of animal destruction going on in order to feed the irrational ivory, rhino horn, pangolin scale and shark fin markets.

Those who buy these products will need to consume fingernails when the animals are all gone. It will have the same effect on their libido and health.

Until next time, enjoy whatever you learn.

from SquareCirclez http://bit.ly/2EI98Ve
via IFTTT

Line integral of a scalar field. Hello friends, today it’s about the line integral of a scalar field. The line integral of a scalar field Solved examples of the line integral of a scalar field Disclaimer: None of these examples are mine. I have chosen these from some book or books. I have also given the...

The post Line integral of a scalar field | Vector integral calculus appeared first on Engineering math blog.

from Engineering math blog http://bit.ly/2HLgtoY

First Encounters

In the mid-1970s, particle physics was hot. Quarks were in. Group theory was in. Field theory was in. And so much progress was being made that it seemed like the fundamental theory of physics might be close at hand.

Right in the middle of all this was Murray Gell-Mann—responsible for not one, but most of the leaps of intuition that had brought particle physics to where it was. There’d been other theories, but Murray’s—with their somewhat elaborate and abstract mathematics—were always the ones that seemed to carry the day.

It was the spring of 1978 and I was 18 years old. I’d been publishing papers on particle physics for a few years, and had gotten quite known around the international particle physics community (and, yes, it took decades to live down my teenage-particle-physicist persona). I was in England, but planned to soon go to graduate school in the US, and was choosing between Caltech and Princeton. And one weekend afternoon when I was about to go out, the phone rang. In those days, it was obvious if it was an international call. “This is Murray Gell-Mann”, the caller said, then launched into a monologue about why Caltech was the center of the universe for particle physics at the time.

Perhaps not as starstruck as I should have been, I asked a few practical questions, which Murray dismissed. The call ended with something like, “Well, we’d like to have you at Caltech”.

A few months later I was indeed at Caltech. I remember the evening I arrived, wandering around the empty 4th floor of Lauritsen Lab—the home of Caltech theoretical particle physics. There were all sorts of names I recognized on office doors, and there were two offices that were obviously the largest: “M. Gell-Mann” and “R. Feynman”. (In between them was a small office labeled “H. Tuck”—which by the next day I’d realized was occupied by Helen Tuck, the lively longtime departmental assistant.)

There was a regular Friday lunch in the theoretical physics group, and as soon as a Friday came around, I met Murray Gell-Mann there. The first thing he said to me was, “It must be a culture shock coming here from England”. Then he looked me up and down. There I was in an unreasonably bright yellow shirt and sandals—looking, in fact, quite Californian. Murray seemed embarrassed, mumbled some pleasantry, then turned away.

With Murray at Caltech

I never worked directly with Murray (though he would later describe me to others as “our student”). But I interacted with him frequently while I was at Caltech. He was a strange mixture of gracious and gregarious, together with austere and combative. He had an expressive face, which would wrinkle up if he didn’t approve of what was being said.

Murray always had people and things he approved of, and ones he didn’t—to which he would often give disparaging nicknames. (He would always refer to solid-state physics as “squalid-state physics”.) Sometimes he would pretend that things he did not like simply did not exist. I remember once talking to him about something in quantum field theory called the beta function. His face showed no recognition of what I was talking about, and I was getting slightly exasperated. Eventually I blurted out, “But, Murray, didn’t you invent this?” “Oh”, he said, suddenly much more charming, “You mean g times the psi function. Why didn’t you just say that? Now I understand”. Of course, he had understood all along, but was being difficult about me using the “beta function” term, even though it had by then been standard for years.

I could never quite figure out what it was that made Murray impressed by some people and not others. He would routinely disparage physicists who were destined for great success, and would vigorously promote ones who didn’t seem so promising, and didn’t in fact do well. So when he promoted me, I was on the one hand flattered, but on the other hand concerned about what his endorsement might really mean.

The interaction between Murray Gell-Mann and Richard Feynman was an interesting thing to behold. Both came from New York, but Feynman relished his “working-class” New York accent, while Gell-Mann affected the best pronunciation of words from any language. Both would make surprisingly childish comments about the other.

I remember Feynman insisting on telling me the story of the origin of the word “quark”. He said he’d been talking to Murray one Friday about these hypothetical particles, and in their conversation they’d needed a name for them. Feynman told me he said (no doubt in his characteristic accent), “Let’s call them ‘quacks’”. The next Monday he said Murray came to him very excited and said he’d found the word “quark” in James Joyce. In telling this to me, Feynman then went into a long diatribe about how Murray always seemed to think the names for things were so important. “Having a name for something doesn’t tell you a damned thing”, Feynman said. (Having now spent so much of my life as a language designer, I might disagree). Feynman went on, mocking Murray’s concern for things like what different birds are called. (Murray was an avid bird watcher.)

Meanwhile, Feynman had worked on particles which seemed (and turned out to be) related to quarks. Feynman had called them “partons”. Murray insisted on always referring to them as “put-ons”.

Even though in terms of longstanding contributions to particle physics Murray was the clear winner, he always seemed to feel as if he was in the shadow of Feynman, particularly with Feynman’s showmanship. When Feynman died, Murray wrote a rather snarky obituary, saying of Feynman: “He surrounded himself with a cloud of myth, and he spent a great deal of time and energy generating anecdotes about himself”. I never quite understood why Murray—who could have gone to any university in the world—chose to work at Caltech for 33 years in an office two doors down from Feynman.

Murray cared a lot about what people thought of him, but would routinely (and maddeningly to watch) put himself in positions where he would look bad. He was very interested in—and I think very knowledgeable about—words and languages. And when he would meet someone, he would make a point of regaling them with information about the origin of their name (curiously—as I learned only years later—his own name, “Gell-Mann”, had been “upgraded” from “Gellmann”). Now, of course, if there’s one word people tend to know something about, it’s their own name. And, needless to say, Murray sometimes got its origins wrong—and was very embarrassed. (I remember he told a friend of mine named Nathan Isgur a long and elaborate story about the origin of the name “Isgur”, with Nathan eventually saying: “No, it was made up at Ellis Island!”.)

Murray wasn’t particularly good at reading other people. I remember in early 1982 sitting next to Murray in a limo in Chicago that had just picked up a bunch of scientists for some event. The driver was reading the names of the people he’d picked up over the radio. Many were complicated names, which the driver was admittedly butchering. But after each one, Murray would pipe up, and say “No, it’s said ____”. The driver was getting visibly annoyed, and eventually I said quietly to Murray that he should stop correcting him. When we arrived, Murray said to me: “Why did you say that?” He seemed upset that the driver didn’t care about getting the names right.

Occasionally I would ask Murray for advice, though he would rarely give it. When I was first working on one-dimensional cellular automata, I wanted to find a good name for them. (There had been several previous names for the 2D case, one of which—that I eventually settled on—was “cellular automata”.) I considered the name “polymones” (somehow reflecting Leibniz’s monad concept). But I asked Murray—given all his knowledge of words and languages—for a suggestion. He said he didn’t think polymones was much good, but didn’t have any other suggestion.

When I was working on SMP (a forerunner of Mathematica and the Wolfram Language) I asked Murray about it, though at the time I didn’t really understand as I do now the correspondences between human and computational languages. Murray was interested in trying out SMP, and had a computer terminal installed in his office. I kept on offering to show him some things, but he kept on putting it off. I later realized that—bizarrely to me—Murray was concerned about me seeing that he didn’t know how to type. (By the way, at the time, few people did—which is, for example, why SMP, like Unix, had cryptically short command names.)

But alongside the brush-offs and the strangeness, Murray could be personally very gracious. I remember him inviting me several times to his house. I never interacted with either of his kids (who were both not far from my age). But I did interact with his wife, Margaret, who was a very charming English woman. (As part of his dating advice to me, Feynman had explained that both he and Murray had married English women because “they could cope”.)

While I was at Caltech, Margaret got very sick with cancer, and Murray threw himself into trying to find a cure. (He blamed himself for not having made sure Margaret had had more checkups.) It wasn’t long before Margaret died. Murray invited me to the memorial service. But somehow I didn’t feel I could go; even though by then I was on the faculty at Caltech, I just felt too young and junior. I think Murray was upset I didn’t come, and I’ve felt guilty and embarrassed about it ever since.

Murray did me quite a few favors. He was an original board member of the MacArthur Foundation, and I think was instrumental in getting me a MacArthur Fellowship in the very first batch. Later, when I ran into trouble with intellectual property issues at Caltech, Murray went to bat for me—attempting to intercede with his longtime friend Murph Goldberger, who was by then president of Caltech (and who, before Caltech, had been a professor at Princeton, and had encouraged me to go to graduate school there).

I don’t know if I would call Murray a friend, though, for example, after Margaret died, he and I would sometimes have dinner together, at random restaurants around Pasadena. It wasn’t so much that I felt of a different generation from him (which of course I was). It was more that he exuded a certain aloof tension, that made one not feel very sure about what the relationship really was.

A Great Time in Physics

At the end of World War II, the Manhattan Project had just happened, the best and the brightest were going into physics, and “subatomic particles” were a major topic. Protons, neutrons, electrons and photons were known, and together with a couple of hypothesized particles (neutrinos and pions), it seemed possible that the story of elementary particles might be complete.

But then, first in cosmic rays, and later in particle accelerators, new particles started showing up. There was the muon, then the mesons (pions and kaons), and the hyperons (Λ, Σ, Ξ). All were unstable. The muon—which basically nobody understands even today—was like a heavy electron, interacting mainly through electromagnetic forces. But the others were subject to the strong nuclear force—the one that binds nuclei together. And it was observed that this force could generate these particles, though always together (Λ with K, for example). But, mysteriously, the particles could only decay through so-called weak interactions (of the kind involved in radioactive beta decay, or the decay of the muon).

For a while, nobody could figure out why this could be. But then around 1953, Murray Gell-Mann came up with an explanation. Just as particles have “quantum numbers” like spin and charge, he hypothesized that they could have a new quantum number that he called strangeness. Protons, neutrons and pions would have zero strangeness. But the Λ would have strangeness -1, the (positive) kaon strangeness +1, and so on. And total strangeness, he suggested, might be conserved in strong (and electromagnetic) interactions, but not in weak interactions. To suggest a fundamentally new property of particles was a bold thing to do. But it was correct: and immediately Murray was able to explain lots of things that had been observed.

But how did the weak interaction that was—among other things—responsible for the decay of Murray’s “strange particles” actually work? In 1957, in their one piece of collaboration in all their years together at Caltech, Feynman and Gell-Mann introduced the so-called V-A theory of the weak interaction—and, once again, despite initial experimental evidence to the contrary, it turned out to be correct. (The theory basically implies that neutrinos can only have left-handed helicity, and that weak interactions involve parity conservation and parity violation in equal amounts.)

As soon as the quantum mechanics of electrons and other particles was formulated in the 1920s, people started wondering about the quantum theory of fields, particularly the electromagnetic field. There were issues with infinities, but in the late 1940s—in Feynman’s big contribution—these were handled through the concept of renormalization. The result was that it was possible to start computing things using quantum electrodynamics (QED)—and soon all sorts of spectacular agreements with experiment had been found.

But all these computations worked by looking at just the first few terms in a series expansion in powers of the interaction strength parameter α≃1/137. In 1954, during his brief time at the University of Illinois (from which he went to the University of Chicago, and then Caltech), Murray, together with Francis Low, wrote a paper entitled “Quantum Electrodynamics at Small Distances” which was an attempt to explore QED to all orders in α. In many ways this paper was ahead of its time—and 20 years later, the “renormalization group” that it implicitly defined became very important (and the psi function that it discussed was replaced by the beta function).

While QED could be investigated through a series expansion in the small parameter α≃1/137, no such program seemed possible for the strong interaction (where the effective expansion parameter would be ≃1). So in the 1950s there was an attempt to take a more holistic approach, based on looking at the whole so-called S-matrix defining overall scattering amplitudes. Various properties of the S-matrix were known—notably analyticity with respect to values of particle momenta, and so-called crossing symmetry associated with exchanging particles and antiparticles.

But were these sufficient to understand the properties of strong interactions? Throughout the 1960s, attempts involving more and more elaborate mathematics were made. But things kept on going wrong. The proton-proton total interaction probability was supposed to rise with energy. But experimentally it was seen to level off. So a new idea (the pomeron) was introduced. But then the interaction probability was found to start rising again. So another phenomenon (multiparticle “cuts”) had to be introduced. And so on. (Ironically enough, early string theory spun off from these attempts—and today, after decades of disuse, S-matrix theory is coming back into vogue.)

But meanwhile, there was another direction being explored—in which Murray Gell-Mann was centrally involved. It all had to do with the group-theory-meets-calculus concept of Lie groups. An example of a Lie group is the 3D rotation group, known in Lie group theory as SO(3). A central issue in Lie group theory is to find representations of groups: finite collections, say of matrices, that operate like elements of the group.

Representations of the rotation group had been used in atomic physics to deduce from rotational symmetry a characterization of possible spectral lines. But what Gell-Mann did was to say, in effect, “Let’s just imagine that in the world of elementary particles there’s some kind of internal symmetry associated with the Lie group SU(3). Now use representation theory to characterize what particles will exist”.

And in 1961, he published his eightfold way (named after Buddha’s Eightfold Way) in which he proposed—periodic-table style—that there should be 8+1 types of mesons, and 10+8 types of baryons (hyperons plus nucleons, such as proton and neutron). For the physics of the time, the mathematics involved in this was quite exotic. But the known particles organized nicely into Gell-Mann’s structure. And Gell-Mann made a prediction: that there should be one additional type of hyperon, that he called the , with strangeness -3, and certain mass and decay characteristics.

And—sure enough—in 1964, the was observed, and Gell-Mann was on his way to the Nobel Prize, which he received in 1969.

At first the SU(3) symmetry idea was just about what particles should exist. But Gell-Mann wanted also to characterize interactions associated with particles, and for this he introduced what he called current algebra. And, by 1964, from his work on current algebra, he’d realized something else: that his SU(3) symmetry could be interpreted as meaning that things like protons were actually composed of something more fundamental—that he called quarks.

What exactly were the quarks? In his first paper on the subject, Gell-Mann called them “mathematical entities”, although he admitted that, just maybe, they could actually be particles themselves. There were problems with this, though. First, it was thought that electric charge was quantized in units of the electron charge, but quarks would have to have charges of 2/3 and -1/3. But even more seriously, one would have to explain why no free quarks had ever been seen.

It so happened that right when Gell-Mann was writing this, a student at Caltech named George Zweig was thinking of something very similar. Zweig (who was at the time visiting CERN) took a mathematically less elaborate approach, observing that the existing particles could be explained as built from three kinds of “aces”, as he called them, with the same properties as Gell-Mann’s quarks.

Zweig became a professor at Caltech—and I’ve personally been friends with him for more than 40 years. But he never got much credit for his aces idea, and after a few years he left particle physics and started studying the neurobiology of the ear—and now, in his eighties, has started a quant hedge fund.

Meanwhile, Gell-Mann continued pursuing the theory of quarks, refining his ideas about current algebras. But starting in 1968, there was something new: particle accelerators able to collide high-energy electrons with protons (“deep inelastic scattering”) observed that sometimes the electrons could suffer large deflections. There were lots of details, particularly associated with relativistic kinematics, but in 1969 Feynman proposed his parton (or, as Gell-Mann called it, “put-on”) model, in which the proton contained point-like “parton” particles.

It was immediately guessed that partons might be quarks, and within a couple of years this had been established. But the question remained of why the quarks should be confined inside particles such as protons. To avoid some inconsistencies associated with the exclusion principle, it had already been suggested that quarks might come in three “colors”. Then in 1973, Gell-Mann and his collaborators suggested that associated with these colors, quarks might have “color charges” analogous to electric charge.

Electromagnetism can be thought of as a gauge field theory associated with the Lie group U(1). Now Gell-Mann suggested that there might be a gauge field theory associated with an SU(3) color group (yes, SU(3) again, but a different application than in the eightfold way, etc.). This theory became known as quantum chromodynamics, or QCD. And, in analogy to the photon, it involves particles called gluons.

Unlike photons, however, gluons directly interact with each other, leading to a much more complex theory. But in direct analogy to Gell-Mann and Low’s 1954 renormalization group computation for QED, in 1973 the beta function (AKA g times psi function) for QCD was computed, and was found to show the phenomenon of asymptotic freedom—essentially that QCD interactions get progressively weaker at shorter distances.

This immediately explained the success of the parton model, but also suggested that if quarks get further apart, the QCD interactions between them get stronger, potentially explaining confinement. (And, yes, this is surely the correct intuition about confinement, although even to this day, there is no formal proof of quark confinement—and I suspect it may have issues of undecidability.)

Through much of the 1960s, S-matrix theory had been the dominant approach to particle physics. But it was having trouble, and the discovery of asymptotic freedom in QCD in 1973 brought field theory back to the fore, and, with it, lots of optimism about what might be possible in particle physics.

Murray Gell-Mann had had an amazing run. For 20 years he had made a series of bold conjectures about how nature might work—strangeness, V-A theory, SU(3), quarks, QCD—and in each case he had been correct, while others had been wrong. He had had one of the more remarkable records of repeated correct intuition in the whole history of science.

He tried to go on. He talked about “grand unification being in the air”, and (along with many other physicists) discussed the possibility that QCD and the theory of weak interactions might be unified in models based on groups like SU(5) and SO(10). He considered supersymmetry—in which there would be particles that are crosses between things like neutrinos and things like gluons. But quick validations of these theories didn’t work out—though even now it’s still conceivable that some version of them might be correct.

But regardless, the mid-1970s were a period of intense activity for particle physics. In 1974, the
J/ψ particle was discovered, which turned out to be associated with a fourth kind of quark (charm quark). In 1978, evidence of a fifth quark was seen. Lots was figured out about how QCD works. And a consistent theory of weak interactions emerged that, together with QED and QCD, defined what by the early 1980s had become the modern Standard Model of particle physics that exists today.

I myself got seriously interested in particle physics in 1972, when I was 12 years old. I used to carry around a copy of the little Particle Properties booklet—and all the various kinds of particles became, in a sense, my personal friends. I knew by heart the mass of the Λ, the lifetime of the , and a zillion other things about particles. (And, yes, amazingly, I still seem to remember almost all of them—though now they’re all known to much greater accuracy.)

At the time, it seemed to me like the most important discoveries ever were being made: fundamental facts about the fundamental particles that exist in our universe. And I think I assumed that before long everyone would know these things, just as people know that there are atoms and protons and electrons.

But I’m shocked today that almost nobody has, for example, even heard of muons—even though we’re continually bombarded with them from cosmic rays. Talk about strangeness, or the omega-minus, and one gets blank stares. Quarks more people have heard of, though mostly because of their name, with its various uses for brands, etc.

To me it feels a bit tragic. It’s not hard to show Gell-Mann’s eightfold way pictures, and to explain how the particles in them can be made from quarks. It’s at least as easy to explain that there are 6 known types of quarks as to explain about chemical elements or DNA bases. But for some reason—in most countries—all these triumphs of particle physics have never made it into school science curriculums.

And as I was writing this piece, I was shocked at how thin the information on “classic” particle physics is on the web. In fact, in trying to recall some of the history, the most extensive discussion I could find was in an unpublished book I myself wrote when I was 12 years old! (Yes, full of charming spelling mistakes, and a few physics mistakes.)

The Rest of the Story

When I first met Murray in 1978, his great run of intuition successes and his time defining almost everything that was important in particle physics was already behind him. I was never quite sure what he spent his time on. I know he traveled a lot, using physics meetings in far-flung places as excuses to absorb local culture and nature. I know he spent significant time with the JASON physicists-consult-for-the-military-and-get-paid-well-for-doing-so group. (It was a group that also tried to recruit me in the mid-1980s.) I know he taught classes at Caltech—though he had a reputation for being rather disorganized and unprepared, and I often saw him hurrying to class with giant piles of poorly collated handwritten notes.

Quite often I would see him huddled with more junior physicists that he had brought to Caltech with various temporary jobs. Often there were calculations being done on the blackboard, sometimes by Murray. Lots of algebra, usually festooned with tensor indices—with rarely a diagram in sight. What was it about? I think in those days it was most often supergravity—a merger of the idea of supersymmetry with an early form of string theory (itself derived from much earlier work on S-matrix theory).

This was the time when QCD, quark models and lots of other things that Murray had basically created were at their hottest. Yet Murray chose not to work on them—for example telling me after hearing a talk I gave on QCD that I should work on more worthwhile topics.

I’m guessing Murray somehow thought that his amazing run of intuition would continue, and that his new theories would be as successful as his old. But it didn’t work out that way. Though when I would see Murray, he would often tell me of some amazing physics that he was just about to crack, often using elaborate mathematical formalism that I didn’t recognize.

By the time I left Caltech in 1983, Murray was spending much of his time in New Mexico, around Santa Fe and Los Alamos—particularly getting involved in what would become the Santa Fe Institute. In 1984, I was invited to the inaugural workshop discussing what was then called the Rio Grande Institute might do. It was a strange event, at which I was by far the youngest participant. And as chance would have it, in connection with the republication of the proceedings of that event, I just recently wrote an account of what happened there, which I will soon post.

But in any case, Murray was co-chairing the event, and talking about his vision for a great interdisciplinary university, in which people would study things like the relations between physics and archaeology. He talked in grand flourishes about covering the arts and sciences, the simple and the complex, and linking them all together. It didn’t seem very practical to me—and at some point I asked what the Santa Fe Institute would actually concentrate on if it had to make a choice.

People asked what I would suggest, and I (somewhat reluctantly, because it seemed like everyone had been trying to promote their pet area) suggested “complex systems theory”, and my ideas about the emergence of complexity from things like simple programs. The audio of the event records some respectful exchanges between Murray and me, though more about organizational matters than content. But as it turned out, complex systems theory was indeed what the Santa Fe Institute ended up concentrating on. And Murray himself began to use “complexity” as a label for things he was thinking about.

I tried for years (starting when I first worked on such things, in 1981) to explain to Murray about cellular automata, and about my explorations of the computational universe. He would listen politely, and pay lip service to the relevance of computers and experiments with them. But—as I later realized—he never really understood much at all of what I was talking about.

By the late 1980s, I saw Murray only very rarely. I heard, though, that through an agent I know, Murray had got a big advance to write a book. Murray always found writing painful, and before long I heard that the book had gone through multiple editors (and publishers), and that Murray thought it responsible for a heart attack he had. I had hoped that the book would be an autobiography, though I suspected that Murray might not have the introspection to produce that. (Several years later, a New York Times writer named George Johnson wrote what I considered a very good biography of Murray, which Murray hated.)

But then I heard that Murray’s book was actually going to be about his theory of complexity, whatever that might be. A few years went by, and, eventually, in 1994, to rather modest fanfare, Murray’s book The Quark and the Jaguar appeared. Looking through it, though, it didn’t seem to contain anything concrete that could be considered a theory of complexity. George Zweig told me he’d heard that Murray had left people like me and him out of the index to the book, so we’d have to read the whole book if we wanted to find out what he said about us.

At the time, I didn’t bother. But just now, in writing this piece, I was curious to find out what, if anything, Murray actually did say about me. In the printed book, the index goes straight from “Winos” to Woolfenden. But online I can find that there I am, on page 77 (and, bizarrely, I’m also in the online index): “As Stephen Wolfram has emphasized, [a theory] is a compressed package of information, applicable to many cases”. Yes, that’s true, but is that really all Murray got out of everything I told him? (George Zweig, by the way, isn’t mentioned in the book at all.)

In 2002, I’d finally finished my own decade-long basic science project, and I was getting ready to publish my book A New Kind of Science. In recognition of his early support, I’d mentioned Murray in my long list of acknowledgements in the book, and I thought I’d reach out to him and see if he’d like to write a back-cover blurb. (In the end, Steve Jobs convinced me not to have any back-cover blurbs: “Isaac Newton didn’t have blurbs on the Principia; nor should you on your book”.)

Murray responded politely: “It is exciting to know that your magnum opus, reflecting so much thought, research, and writing, will finally appear. I should, of course, be delighted to receive the book and peruse it, and I might be able to come up with an endorsement, especially since I expect to be impressed”. But he said, “I find it difficult to write things under any conditions, as you probably know”.

I sent Murray the book, and soon thereafter was on the phone with him. It was a strange and contentious conversation. Murray was obviously uncomfortable. I was asking him about what he thought complexity was. He said it was “like a child learning a language”. I asked what that meant. We went back and forth talking about languages. I had the distinct sense that Murray thought he could somehow blind me with facts I didn’t know. But—perhaps unfortunately for the conversation—even though A New Kind of Science doesn’t discuss languages much, my long efforts in computational language design had made me quite knowledgeable about the topic, and in the conversation I made it quite clear that I wasn’t convinced about what Murray had to say.

Murray followed up with an email: “It was good to talk with you. I found the exchange of ideas very interesting. We seem to have been thinking about many of the same things over the last few years, and apparently we agree on some of them and have quite divergent views on others”. He talked about the book, saying that “Obviously, I can’t, in a brief perusal, come to any deep conclusions about such an impressive tome. It is clear, however, that there are many ideas in it with which, if I understand them correctly, I disagree”.

Then he continued: “Also, my own work of the last decade or so is not mentioned anywhere, even though that work includes discussions of the meaning and significance of simplicity and complexity, the role of decoherent histories in the understanding of quantum mechanics, and other topics that play important roles in A New Kind of Science”. (Actually, I don’t think I discussed anything relevant to decoherent histories in quantum mechanics.) He explained that he didn’t want to write a blurb, and ended: “I’m sorry, and I hope that this matter does not present any threat to our friendship, which I hold dear”.

As it turned out, I never talked to Murray about science again. The last time I saw Murray was in 2012 at a peculiar event in New York City for promising high-school students. I said hello. Murray looked blank. I said my name, and held up my name tag. “Do I know you?”, he said. I repeated my name. Still blank. I couldn’t tell if it was a problem of age—or a repeat of the story of the beta function. But, with regret, I walked away.

I have often used Murray as an example of the challenges of managing the arc of a great career. From his twenties to his forties, Murray had the golden touch. His particular way of thinking had success after success, and in many ways, he defined physics for a generation. But by the time I knew him, the easy successes were over. Perhaps it was Murray; more likely, it was just that the easy pickings from his approach were now gone.

I think Murray always wanted to be respected as a scholar and statesman of science—and beyond. But—to his chagrin—he kept on putting himself in situations that played to his weaknesses. He tried to lead people, but usually ended up annoying them. He tried to become a literary-style author, but his perfectionism and insecurity got in the way. He tried to do important work in new fields, but ended up finding that his particular methods didn’t work there. To me, it felt in many ways tragic. He so wanted to succeed as he had before, but he never found a way to do it—and always bore the burden of his early success.

Still, with all his complexities, I am pleased to have known Murray. And though Murray is now gone, the physics he discovered will live on, defining an important chapter in the quest for our understanding of the fundamental structure of our universe.

from Stephen Wolfram Blog http://bit.ly/2Ib2nMm

This spring, Hyundai Motor America (HMA) announced a $250,000 donation to Montgomery Public Schools (MPS) for STEM education. The Hyundai ST Math® Initiative will now benefit over 3,000 students from five schools in MPS including Brewbaker, Catoma, Morningview, Seth Johnson, and T.S. Morris Elementary.

HMA has partnered with MIND Research Institute since 2011 and has committed over $2 million to our ST Math program in the eight years since. This particular donation is very special for HMA though, because it will directly impact students in their own backyard.

Our goal here is to be a trusted partner in this community and other communities around the nation. This nation depends on a skilled labor force, and research shows that when a child has access to STEM education, we will have a stronger student, and it will contribute to a life-long love of learning.

- Zafar Brooks, HMA

Hyundai Motor Manufacturing Alabama (HMMA) has called the city of Montgomery home for nearly 15 years and employs over 3,000 members of the community. Hyundai also directly supports a host of suppliers, local businesses and organizations throughout the city. This latest donation not only continues HMA’s commitment to education, it also furthers its commitment to the community. So, what better way to kick off the program than by bringing the Montgomery community together?

On May 21, 2019, HMA executives invited city dignitaries, school officials and other special guests to celebrate with them. The day started at their HMMA plant. Guests, including our own Jim Sidick, Regional Vice President of Partnerships, were given a quick tour followed by a luncheon.

Safety goggles... check! ✔️ Jim Sidick, a Regional Vice President of Partnerships here at MIND, is ready for a fun day with our partner, @Hyundai. They're up to something great in Montgomery, AL! Stay tuned... #SocialImpact #CSR pic.twitter.com/w5QaPfQGaH

— MIND Research Institute (@MIND_Research) May 21, 2019

The group then headed over to the Catoma Elementary school library for a press conference and check presentation. Clare Weil, MPS School Board President, welcomed attendees. One of those attendees was Dr. Bernice A. King, CEO of The King Center For Non-violent Social Change and youngest child of Martin Luther King Jr. and Coretta Scott King.

Coming together: City, county and education leaders join @Hyundai executives and special guest @BerniceKing at Montgomery's Hyundai plant as the company commits $250,000 to five MPS schools for a STEM program. #MPSMovingForward pic.twitter.com/ykkIwFymm5

— MontgomeryCoSchools (@MPSAL) May 23, 2019

Zafar Brooks, Director of Corporate Social Responsibility and Diversity & Inclusion at HMA, then presented a check to Dr. Ann Roy Moore, MPS Superintendent.

Zafar Brooks (right) of HMA presents a check for $250,000 to Montgomery Public Schools to further STEM education through ST Math.

One of the most impactful moments of the day came when Saige Williams, 4th grade student, addressed the crowd and spoke about the importance of math education.

Saige Williams (left) and her friend hold MIND’s new MathMINDs Games: South of the Sahara game boxes, a gift from HMA to MPS.

Jim Sidick also had the opportunity to speak on behalf of MIND. He thanked Zafar and HMA for bringing ST Math to Montgomery.

It’s going to support teachers and their understanding and help children learn mathematics in a conceptual way.

- Jim Sidick, MIND

The event concluded with remarks by Todd Strange, Mayor of Montgomery; Elton Dean, Commissioner Chairman; Willie Durham, Montgomery Area Chamber of Commerce Chairman; and Robert Burns, Director of HR & Administration at HMMA.

The Montgomery Area Chamber of Commerce commends our industry partners at Hyundai Motor America for this generous gift to the Montgomery Public School system. Partnership means preparing to succeed together, and the ST Math Initiative will provide a tremendous value as Montgomery focuses on preparing a workforce for a higher wage, skilled work environment in a diverse, innovative, tech-driven economy.

- Willie Durham, City of Montgomery

With this latest donation, HMA is now bringing the power of ST Math to 72 schools, 23,258 students and 1,000 teachers throughout the nation.

Thank you, Hyundai Motor America, for your continued partnership to elevate student achievement and develop the next generation of innovators and problem solvers!

Check out additional coverage of the event:

• Hyundai donates $250,000 to Montgomery Public Schools for STEM education [Video]
• Hyundai donates $250K to MPS for STEM programs [Video]
• Hyundai gives $250,000 for new math program at 5 MPS elementary schools

from MIND Research Institute Blog http://bit.ly/2EHAk6k

submitted by /u/AutoModerator
[link] [comments]

from math http://bit.ly/2Wc5e1E