Mathematicianadda

Problem

Let $f(x)\in L^2(-\infty,\infty)$. Prove that $$ \lim_{n\to\infty}\int_{-\infty}^\infty f(x)f(x+n) dx=0. $$

My attempt

Let $N\in\mathbb{N}$ and $f_N(x):=f(x)\chi_{[-N,N]}(x)$.

For any $n\in\mathbb{N}$, consider

$$ \begin{split} \int_{-\infty}^\infty f(x)f_N(x+n)dx&=\int_{-\infty}^\infty f(x)f(x+n)\chi_{[-N,N]}(x+n)dx\\ &=\int_{-\infty}^\infty f(x)f(x+n)\chi_{[-N-n,N-n]}(x)dx\\ &=\int_{-N-n}^{N-n}f(x)f(x+n)dx \end{split} $$

This is where I get stuck.

We know for a.e. $x\in\mathbb{R}$ that $\lim_{n\to\infty} f(x+n)=0$. Thus, if I were allowed to interchange limit and integral, I would get the desired conclusion. I tried Dominated Convergence Theorem, but could not find a way to dominate the integrand by an integrable function not depending on $n$.

Maybe there is a different approach. Any hints? I'd like to be able to say the absolute value of the above integral is less than any $\varepsilon>0$ for $n$ large enough, and then since $N$ is arbitrary, the conclusion follows.

from Hot Weekly Questions - Mathematics Stack Exchange
briemann

submitted by /u/Greenface1998
[link] [comments]

from math https://ift.tt/2ZoMgn5 https://ift.tt/eA8V8J

submitted by /u/dancingbanana123
[link] [comments]

from math https://ift.tt/3gexhD2 https://ift.tt/eA8V8J

Suppose $S_R$ - is the set of all total recursive bijections on $\mathbb{N}$. It is not hard to see that this set forms a group with respect to composition, and that $|S_R| = \aleph_0$. Is $S_R$ finitely generated?

The group $S_R$ contains the group $S_\infty$ (the group of finitely based bijections) as its subgroup, which is infinitely generated. However, there exists $S_\infty < H \leq S_R$, such that $H$ is finitely generated. The $H$ can be described as $\langle (01), f \rangle$, where $f$ is defined by formula:

$$f(x) = \begin{cases} 0 & \quad x = 0 \\ 2 & \quad x = 1 \\ x + 2 & \quad x \geq 2 \text{ and is even} \\ x - 2 & \quad x \geq 2 \text{ and is odd} \end{cases}$$

Indeed, $\forall x = 2n+1$ $(0x)=(01)f^{n}$ and $\forall x = 2n$ $(0x)=(01)f^{-n}$. Hovever, this does not give us the answer to the question as $H$ is most likely a proper subgroup of $S_R$ (though, i do not know for sure).

from Hot Weekly Questions - Mathematics Stack Exchange
Yanior Weg

submitted by /u/battle-obsessed
[link] [comments]

from math https://ift.tt/31vFb75 https://ift.tt/eA8V8J

Lagrange's four square theorem states that any natural number $n$ can be written as the sum of the square of 4 other integers. For most values of $n$, there are multiple square combinations that work. For example, $16=4^2$ and also $16=2^2 + 2^2 + 2^2 + 2^2$. Is there a name for the solution where first term is as large as possible, the second term is as large as possible (given the value of the first term), and so on? For 16, this would be the $4^2$ solution. I'd still want no more than 4 nonzero terms.

Has this solution been discussed anywhere? I like this solution because it's unique.

Also, would that solution be equivalent to the solution with the fewest nonzero terms?

If no name for this solution exists, what name would you suggest? Names that occur to me are the minimum entropy solution, or the maximum bias solution.

from Hot Weekly Questions - Mathematics Stack Exchange
user3433489

Check out this Advanced Knowledge Problem of the Week.
Be sure to let us know how you solved it in the comments below or on social media!

Solution below.



from The Center of Math Blog https://ift.tt/2VAutbH

While studying Linear Algebra from Hoffman Kunze I have following two questions :

I.3. Matrices and Elementary Row Operations

One eannot fail to notice that in forming linear combinations of linear equations there is no need to continue writing the "unknowns' $x_{1}, \ldots, x_{n},$ since one actually computes only with the coefficients $A_{i j}$ and the sealars $y_{i} .$ We shall now abbreviate the system (1-1) by $$AX=Y$$ where $$A=\begin{bmatrix}A_{11}&\cdots&A_{1n}\\\vdots&&\vdots\\A_{m1}&\cdots&A_{mn}\end{bmatrix}\\X=\begin{bmatrix}x_1\\\vdots \\x_n\end{bmatrix}\text { and }Y=\begin{bmatrix}y_1\\\vdots\\y_m\end{bmatrix}$$ We call $A$ the matrix of coefficients of the system. Strictly speaking, the rectangular array displayed above is not a matrix, but is a representation of a matrix. An $m \times n$ matrix over the field $F$ is a function $A$ from the set of pairs of integers $(i, j), 1 \leq i \leq m, 1 \leq j \leq n,$ into the field $F$. The entries of the matrix $A$ are the scalars $A(i, j)=A_{i j},$ and quite often it is most convenient to describe the matrix by displaying its entries in a rectangular array having $m$ rows and $n$ columns, as above. Thus $X$ (above) is, or defines, an $n \times 1$ matrix and $Y$ is an $m \times 1$ matrix. For the time being, $A X=Y$ is nothing more than a shorthand notation for our system of linear equations. Later, when we have defined a multiplication for matrices, it will mean that $Y$ is the product of $A$ and $X$

Questions->

(1) Why in 2nd paragraph author wrote that the rectangular array displayed above is not a matrix?

(2) In 2nd line of 2nd paragraph author wrote the definition of matrix. How is a matrix a function from set of pair of integers into the field? To me this defination given contradicts the defination given on Wikipedia and I can't understand it.

Definition on Wikipedia: https://en.m.wikipedia.org/wiki/Matrix_(mathematics)

Can kindly anyone explain why I am confused .

from Hot Weekly Questions - Mathematics Stack Exchange
user795826

submitted by /u/LaZzoFTW
[link] [comments]

from math https://ift.tt/2CPtlKA https://ift.tt/eA8V8J

This article features contributions from MIND Research Institute's Director of Product, Twana Young, and Senior User Experience Researcher, Alesha Arp.

Individual vs Group Goals

I learned the value of individual goal setting as a high school cross-country and track runner. My coach, Dave Donaldson, taught all of his runners to set goals and then aim beyond them. His philosophy was that you didn’t want to just run to the top of the hill, but over the top.

Today, my goals are not as speedy, but they’re no less “over the top” and I am always heartened when I visit schools where students can articulate their goals and can share how they’re working toward achievement.

In the current version of ST Math, the primary metric is percent progress. Students across the country are recognized on class bulletin boards and in school assemblies for achieving a targeted progress percentage, whether that’s 25% per quarter, or 70% by spring break, or 100% by the end of the school year. These celebrations are wonderful and the sense of pride that students have in this accomplishment is evident by their smiles.

However, focusing on one single metric for all students can be exclusionary.  Sometimes a one-size-fits-all goal centers too much on extrinsic motivation. 

Oftentimes it’s the stars on the bulletin board, or the popsicle party at the end of the year that drives kids to reach their percent progress goal. If you ask the student the value of achieving that goal, they’re not going to tell you what they learned about problem solving, goal setting, and perseverance. They’re going to tell you they wanted to attend the popsicle party.

If a student doesn’t reach the school- or class-wide 25% progress mark by the end of the first quarter (or 33% for the trimester), they start every subsequent grading period behind, and the hill they need to climb to overcome that deficit can be insurmountable. Some never catch up.

By the same token, some students reach 100% quickly, and then have no motivation to deepen their exploration or understanding of the concepts.

I spoke with a teacher in Oakland, CA early this spring who lamented that the kids who get recognized at their weekly assembly are typically those students who have access to devices and internet at home. She feels this celebrates the “haves” and leaves out the “have-nots.” While their students without device access at home benefit from the time they play ST Math in school, it is not likely—with their current program implementation—that these students will reach 100% progress.

The administrator, curriculum coach, and teachers are all working to alter their implementation, but until that comes to fruition, a vast majority of the students are striving toward an unattainable goal. I would propose differentiating and encouraging students to set and track their own goals. 

Revising the Focus

With the redesign of ST Math due out for the 2020-21 school year, differentiation will be easier for teachers to employ and students will have direct visibility into metrics they can influence. But we do not need to wait until next school year to individualize student goals.

With students now learning at home, individual accountability gives kids more control at a time when they likely feel they don’t have a lot of control.

Tracking Individual Accountability

To better understand what is available for parents and teachers working remotely to use now with their kids, I invited Twana Young, MIND’s Director of Instructional Development, into the conversation. Twana is one of our thought leaders here at MIND Research Institute. She brings a rich background to her work as an educator and former district administrator experienced in developing curricular programs at the local, state, and national level.

Twana has rich experience building, supporting, and monitoring STEM-rich environments. I asked Twana, “How can teachers foster individual accountability for their students now?”

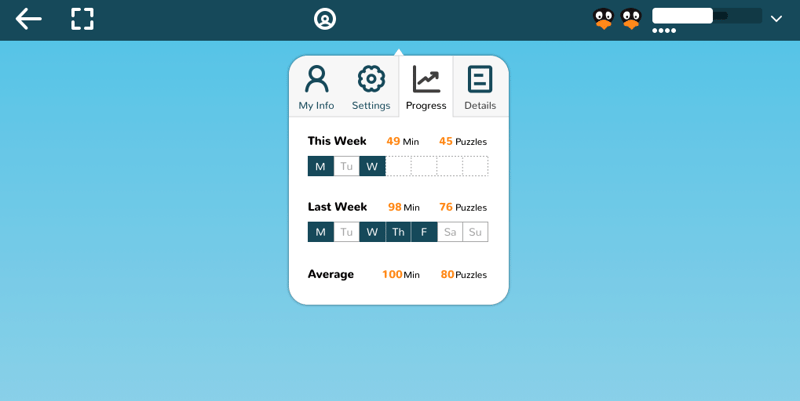
With so much talk of what students are missing out on by not being in school, there are some great opportunities that exist to build student agency, accountability, and confidence in mathematics. In our current ST Math program when students complete their session, they are taken to their My Accomplishment’s page.

 This page highlights the amount of time, the progress, number of puzzles, and levels the students mastered during this session.

Having this type of explicit data provides a great opportunity for students to identify appropriate goals, set action steps to achieve the goals,  monitor their progress toward the goals, and learn to adjust the goals based on the data.  

“Are there ways parents can support their students’ learning with little management time?”

To support student goals we have developed an ST Math Usage calendar. Students can identify a goal at the beginning of the week based on the number of minutes of  ST Math or the number of days to play ST Math. Students can track their goals by recording their progress on the ST Math Usage calendar. Students should be encouraged to share their goals with family and discuss how they plan to achieve them. 

Download the Spanish version>>

Twana cautioned though, that usage goals are not the only way students can track achievement.

In addition to usage goals, it is important for students to set and work toward academic goals. Because ST Math is a mastery-based visual, spatial program, students are able to have confidence that they are growing in mathematical understanding as they play.

They may set academic goals related to number of objectives completed, math concepts learned, hurdles overcome, classroom connections made, etc. As students communicate their academic goals, they should also communicate what they are learning. This will support them in developing a deep understanding of content, transferring and applying knowledge, and learning how to effectively communicate.

Math journals are great resources for students to reflect on their ST Math session, process their thinking, communicate what they have learned, and monitor their progress toward their academic goals.  

Empowering Students to Set and Achieve Goals

Thinking back again to my high school running days, I can assure you, I never would have run a sub-5:30 mile for my coach, no matter how supportive and encouraging he was. 

• I had to set that goal for myself, and do the work to consistently run a mile in under five-and-a-half minutes.
• I had to solve the problem of not having enough practice-time after school, by running extra practices in the dark before school.
• I had to persevere through the 40 repetitions up and down the nearby junior college stadium steps each week.

Helping students set, own, and achieve individual goals is so much more powerful than giving them stars and popsicles. Had my coach set a team-goal some would have achieved it, while others wouldn’t have come close. Had he set the sub-5:30 goal for me in my freshman year, I’d have ended that season well-short and feeling unaccomplished. 

I asked Twana, “What are the greatest advantages to kids being accountable for their learning that you’ve seen?”

When students play ST Math games, they are not only deepening their understanding of math concepts, they are developing critical problem-solving skills that will lead to lasting success. Setting goals is a great way to build on that and increase opportunities for student agency and accountability. Students will not only develop confidence but will more readily recognize their progress and growth. 

Goal setting can also strengthen students’ ability to communicate about what they have learned and accomplished, as well as identify areas in which they would like to improve. In addition, students will learn how to manage their time better, focus on challenges, and develop plans to overcome them. 

“Wow, these are the skills all of our kids will need to succeed in the workforce of tomorrow!”

Individual Goals Support Differentiation and Inclusivity

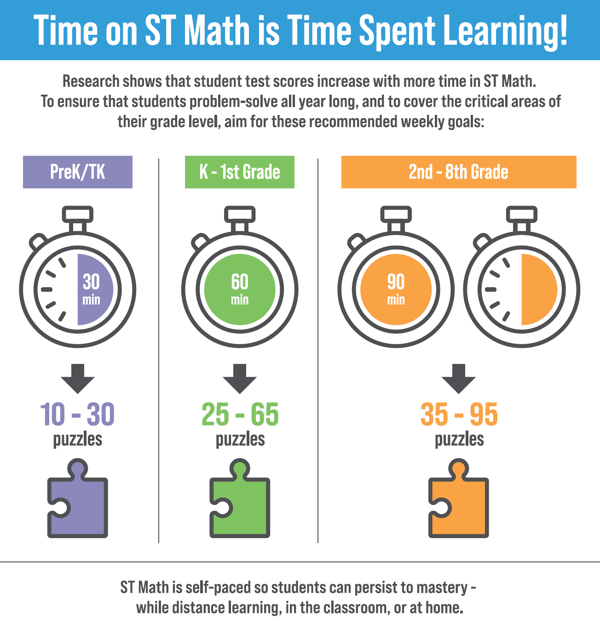
Next year’s redesigned ST Math will shift the focus to minutes spent and puzzles completed (a puzzle is one math problem within a level of a game). Regardless of what content students are playing, they will be able to see that they have spent x number of minutes and achieved y number of puzzles. This will allow for differentiated learning in tandem with individual goal setting and accountability.

Teachers will have the ability to assign content from any grade level to any student or group of students. For students struggling with a concept, the teacher can assign scaffolding concepts to build up their foundational skills. For students who excel and need a greater challenge a teacher might offer more advanced concepts. This will allow different students to traverse varied paths through the ST Math content. 

Students at all points in the learning curve—those who struggle to those who excel—will be able to set goals based on the available metrics: minutes spent, and puzzles achieved. Students are, after all, individuals. The student who has trouble staying focused might have a very different goal than the student who speeds through without retention or the student who seeks help at the first sign of difficulty.

Just like I did with my dark-morning workouts, a student can control the time and the focus they put into ST Math.  Even a student who doesn’t have device access from home, can be most productive with their allotted time by signing in and getting to work right away. They could set a puzzles per minute goal and work to achieve that. 

My first goal when I joined the cross-country team was to break 8 minutes in the mile. Over time, as each goal was attained, a new goal was set.

If students have an achievable minutes goal and awareness of the average number of puzzles they typically achieve, they can work to increase that week over week. If they’re spending time visiting with their seatmate, this will be evidenced in that ratio; they can then adjust and can take full advantage of the time allotted by spending each minute productively. 

Running the same mile-time on a hilly cross-country course, or in mud is not as achievable as running it flat-out on a track. 

When students are met with a really difficult concept, and their puzzle count drops, they can talk about that and adjust. Kids can learn to adjust their goal for the conditions and readjust when conditions are more favorable. 

A student who needs scaffolding content to build their foundation, likely won’t complete all the grade-level content in that school year, however they can improve their math competency, problem-solving abilities, and their perseverance by setting and achieving their own goals.

I have visited classrooms where they haven’t yet figured out how to get 60 or 90 minutes of time worked into their weekly schedule. But motivated students opt-in to ST Math during “free-tech” time or “free-learning” time—which usually happens on Fridays when teachers are wrapping up lessons with students who were absent during the week. If students have ownership of and accountability for their own goals, they are more likely to opt-in. 

Additional Resources

• New ST Math: Coming June 2020!
• Redesigning the New ST Math to Drive Actionable Data
• Adaptive and Supportive Learning with ST Math
• Success and Failure: How Growth Mindset Can Change Education
• Podcast: Being Driven by Actionable Data

 

from MIND Research Institute Blog https://ift.tt/3iffu0v
Alesha Arp

Let $P_{m,n}=P_{m,n}(x,y)$ be a polynomial family. Here is some initial terms $$ P_{0,0}=1, P_{1,0}=2x, P_{0,1}=2y, P_{1,1}=8xy.$$ I know that the polynomials for any $m,n \geq 0$ satisfy the five differential recurrence relations \begin{align} &n \frac{\partial P_{m,n-1}}{\partial x}=m \frac{\partial P_{m-1,n}}{\partial y},\\ & x \frac{\partial P_{m,n}}{\partial x}=m P_{m,n}+m\frac{\partial P_{m-1,n}}{\partial x},\\ & y\frac{\partial P_{m,n}}{\partial x}=m P_{m-1,n+1}+n \,\frac{\partial P_{m,n-1}}{\partial x},\\ & y \frac{\partial P_{m,n}}{\partial y}=n P_{m,n}+n\frac{\partial P_{m,n-1}}{\partial y},\\ & x\frac{\partial P_{m,n}}{\partial y}=n P_{m+1,n-1}+m \,\frac{\partial P_{m-1,n}}{\partial y}. \end{align}

Also. they satisfied the differential equation $$ (1-x^2) \frac{\partial^2 P_{m,n}}{\partial x^2} -x y \frac{\partial^2 P_{m,n} }{\partial x \partial y} -(n+3) x \frac{\partial P_{m,n}}{\partial x }+m y \frac{\partial P_{m,n}}{\partial y }+m(m+n+2) P_{m,n}=0, $$ for any $m,n.$

I need to eliminate all the derivatives and get pure recurrence relations for $P_{m,n}$.

By numeric expеriments I guess such recurrence relations $$ 2 (1{+}m{+}n) x P_{m,n}=P_{m+1,n}{-}n(n{-}1)P_{m+1,n-2}{+m(m+2n+1)}P_{m-1,n},\\ 2 (1{+}m{+}n) y P_{m,n}=P_{m,n+1}{-}m(m{-}1)P_{m-2,n+1}{+}n(n+2m+1)P_{m,n-1} $$ but I still cant prove it.

Any help?

from Hot Weekly Questions - Mathematics Stack Exchange
Leox

A while ago, my son did the Prime Climb colouring sheet.

We’re doing Prime Climb colouring. Sheet from @MathforLove here: https://t.co/O156rMY6An #tmwyk pic.twitter.com/dyhC2pBZGa

— Peter Rowlett (@peterrowlett) April 20, 2020

The idea is to colour each number. Primes are given a new, single colour. Then composite numbers are broken into segments, which are coloured using the colours of their prime factors.

It came out like this.

Recently, I was encouraged to try LuaTeX, which is a replacement for pdflatex that has better font support and means you can run Lua code in your LaTeX documents.

Looking for a project to try running some Lua code in a LaTeX document, and inspired by Andrew Stacey’s mention of the Sieve of Eratosthenes, I wrote some Lua code to generate TikZ code that draws grids like the one above. Here are some examples.

I had a second go with Lua and played around with primes, using it to get tikz to draw things like this. pic.twitter.com/wHO0UN3FpO

— Peter Rowlett (@peterrowlett) June 27, 2020

So now my son has a print out of my hundred grid next to the one he coloured in on his wall. He complained about my choice of colours, especially for 11.

You can look at the code I wrote on GitHub as drawing-primes – GitHub is something else new I’m trying. Oh, and I learned a bit of markdown today to write the readme file – so it’s all new coding things for me at the moment!

from The Aperiodical https://ift.tt/2BokKyc
Peter Rowlett

Consider a Young diagram defined as follows:

A Young diagram (also called a Ferrers diagram, particularly when represented using dots) is a finite collection of boxes, or cells, arranged in left-justified rows, with the row lengths in non-increasing order. Listing the number of boxes in each row gives a partition $\lambda$ of a non-negative integer $n$, the total number of boxes of the diagram.

For example we may write 1+4+5=10:

Question: Are there higher-dimensional versions, using cubes, such that the "faces" of the diagram are each themselves Young diagrams?

Here is an example, with three distinct faces, each representing diagrams: 1+2+3+3, 2+2+3+3, and 0+0+4+4. The faces are the Young diagrams on the faces of the cube in this case. It has 6 faces, and three pairs of (up,right,in), each a Young diagram. In 2d, there is only 1 face (1 diagram). In 3d, one has a cube with six faces, but only three are unique diagrams. One diagram in the 3d case is forced from the other two (up,right,up,right....up and up,up,in,in,up lead to the other necessarily being right,right,in,in,right).

If so, is there a way of writing an integer in terms of the diagram, in the same way as an integer can be represented via one of many Young diagrams (i.e. integer partitions)? This would represent a restricted integer partition, but in a relatively unusual way.

For example the image below would represent the integer partition ((2+2) + (3+3)) + ((2+2) + (3+3)) = 20.

from Hot Weekly Questions - Mathematics Stack Exchange
apkg

factor $ab^3 - a^3 b + bc^3 - b^3 c + ca^3 - c^3 a$ I used the factor theorem to get factors $f(a, b, c)=(a-b)(b-c)(a-c)g (a, b, c)$ for some polynomial $g (a, b, c)$. How can I continue using this method? (sorry for the previously messed up question I'm new to this website and didn't fully understand the guidelines).

from Hot Weekly Questions - Mathematics Stack Exchange
user5678

submitted by /u/Drakejeff666
[link] [comments]

from math https://ift.tt/3icIeqC https://ift.tt/eA8V8J

submitted by /u/htripathi6
[link] [comments]

from math https://ift.tt/3ievIqt https://ift.tt/eA8V8J

Let $Frege(X)$ be the set of all equivalence classes of subsets of $X$ under equivalence relation bijection. formally:

$Frege(X)= \{\{Y \subseteq X: |Y|=|Z|\}: Z \subseteq X \}$

Where $||$ is cardinality function defined after Scott's.

My question is about the following statement:

$\forall X: |Frege(X)| \leq |X|+1$

Is it equivalent to the axiom of choice over the rest of axioms of $\sf ZF$?

More precisely can $\sf ZF$ plus the above statement prove the axiom of choice?

Afternote: To spell the above without invoking Scott's cardinality just replace $|Y|=|Z|$ by $\exists f(f: Y \to Z \land f \text{ is a bijection})$, and replace $|Frege(X)| \leq |X| + 1$ by $\exists g (g: Frege(X) \to X \cup \{X\} \land g \text{ is an injection})$

from Hot Weekly Questions - Mathematics Stack Exchange
Zuhair

Assuming $P(x)$ is a polynomial, can one deduce that $P(x)$ is a polynomial of degree $0$ or $1$ from the following condition: $$2P(x) = P\bigg(x-\frac{2^k}{n}\bigg) +P\bigg(x+\frac{2^k}{n}\bigg), \ \ \forall x $$ where $n$ is a fixed positive integer and $k\in\mathbb{N}\cup\{0\}$.

The identity gives a feeling like the values of $P(x)$ is "equally distributed" and its graph illustrates a straight line since $$P(x) = \cfrac{P\bigg(x-\frac{2^k}{n}\bigg) +P\bigg(x+\frac{2^k}{n}\bigg)}{2}$$ so its value at $x$ is an arithmetic mean of its values at $x-\frac{2^k}{n}$ and $x+\frac{2^k}{n}$. I don't have a potential argument though.

Update: I've just come up with a solution (posted below). Even if it is correct (verifications would be awesome), I'm still open for solutions with different approaches. Thanks.

from Hot Weekly Questions - Mathematics Stack Exchange
VIVID

I am trying to find the integer $n$ such that \begin{align} 1-a c^{n-1} \ge \exp(-\frac{1}{n}) \end{align} where $a>0$ and $c \in (0,1)$.
I know that finding it exactly is difficult. However, can one find good upper and lower bounds it.

It tried using lower bound $\exp(-x) \le 1-x+\frac{1}{2}x^2$. However, it didn't really work.

from Hot Weekly Questions - Mathematics Stack Exchange
Lisa

Prove that $$\lim_{n\to \infty}\left(\ln 2 -\left(-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\cdots +\frac{(-1)^n}{n}\right)\right)^n =\sqrt{e}$$

I happened to encounter this problem proposed by Mohammed Bouras,Morocco in the facebook group of Romanian mathematical Magazine

As per the title, I think the limit of the problem depends upon the parity of $n$. That is,if $n$ is even, the limit is $\frac{1}{\sqrt e}$ otherwise as stated.

My query is, Does the parity indeed matters for this problem? And if it matters what should be the conclusion for limit of the problem?

Here is my try

we will show that the there exist two different limits for above problem.

For $0< x\leq 1$, we define the functions $$f(x)=\ln(1+x),\; \displaystyle g(x)=\sum_{k=1}^n \frac{(-x)^k}{k+1}$$ and we note that $$f(x)-g(x) = x-\sum_{k=2}^{\infty}(-1)^{k+n} \frac{x^{k+n}}{k+n}=x+\sum_{k=2}^{\infty} (-1)^{k+n} \int_0^x t^{k+n-1}dt =x+(-1)^n\int_0^x t^n\left(\sum_{k=1 }^{\infty}(-1)^k t^{k-1} \right)dx=x-(-1)^n\int_0^x\frac{t^n}{1+t} dt$$ hence for $x=1$ we have then $$f(1)-g(1)=\ln(2)-\sum_{k=1}^{\infty}\frac{(-1)^k}{k+1}=1-(-1)^n\int_0^1\frac{t^n}{1+t}dt$$ Note that latter integral is know result however,here we shall derive it and we shall show that

$$\displaystyle \lim_{n\to\infty}(f(1)-g(1))^n =\begin{cases} \sqrt{e}\; \text{if } \, n\in 2n-1 \\ \frac{1}{\sqrt{e}} \; \text{otherwise}\end{cases}$$

We solve the following integral for any $n>0$. By polynomial long division it is trivial to note that $$\int_{0}^1\frac{t^{n}}{t+1}dt=(-1)^n\int_0^1\left(\frac{1}{t+1}-\sum_{0\leq j\leq n}(-1)^j t^{j-1}\right)dt$$ and hence on integrating $\displaystyle \int_0^1\frac{t^{n}}{1+t}dt$ $$=(-1)^n\left(\log(2) -\sum_{1\leq j\leq n} \frac{(-1)^{j+1}}{j}\right)=2^{-1}\left(\psi\left(\frac{n+1}{2}\right)-\psi\left(\frac{2n+1}{2}\right)\right)=\frac{1}{2}\left(H_{\frac{n}{2}}-H_{\frac{n-1}{2}}\right)$$ Further we note that $H_n\approx \gamma +\ln n +\frac{1}{2n}-O(n^{-2})$ with which we deduce that $$H_{\frac{n}{2}} -H_{\frac{n-1}{2}} \approx \frac{1}{n}-\ln\left(\frac{n-1}{n}\right)+\frac{1}{n-1}$$ for all $n>1$ and hence $H_{\frac{n}{2}} -H_{\frac{n-1}{2}} \to \frac{1}{n}$as $n$ gets larger. Thus we have for $$\lim_{n\to\infty}(f(1)-g(1))^n= \lim_{n\to\infty} \left(1-\frac{(-1)^n}{2n}\right)^{n}=e^{-\frac{(-1)^n}{2}} =\sqrt{e^{-(-1)^n}}$$ therefore if $n$ is even we have limit as $\displaystyle \frac{1}{\sqrt{e}}$ and if $n$ is odd we have limit $ \displaystyle \sqrt{e}$.

Since we have two different limits. Does it have limit ?

Thank you

from Hot Weekly Questions - Mathematics Stack Exchange
Naruto

In classical electrodynamics, given the shape of a wire carrying electric current, it is possible to obtain the magnetic field configuration $\mathbf{B}$ via the Biot-savart law. If the wire is a curve $\gamma$ parametrized as $\mathbf{y}(s)$, where $s$ is the arc-length, then

$$ \mathbf{B}(\mathbf{x}) = \beta \int_\gamma \dfrac{ d\mathbf{y}\times(\mathbf{x} - \mathbf{y}) }{|\mathbf{x} - \mathbf{y}|^3} = \beta \int_\gamma ds \dfrac{ \mathbf{y}'(s) \times(\mathbf{x} - \mathbf{y}(s)) }{|\mathbf{x} - \mathbf{y}(s)|^3} \, , $$

where $\beta $ is just a physical constant proportional to the current in the wire.

Another application of the Biot-Savart law is to find the velocity field $\mathbf{v}$ around a bent vortex line in a fluid, in the approximation of incompressible and irrotational fluid flow (i.e. $\nabla \cdot \mathbf{v} =0$ and $\nabla \times \mathbf{v} =0$ almost everywhere) and very-thin diameter of the vortex core. In fact, by demanding that the vorticity of the fluid is concentrated on the vortex core (i.e. it is distributed as a Dirac delta peaked on the vortex core),

$$ \mathbf{w}(\mathbf{x}) = \nabla \times \mathbf{v}(\mathbf{x})= c \int_\gamma ds \, \mathbf{y}'(s)\, \delta( \mathbf{x} - \mathbf{y}(s)) \, , $$

we have that the Helmholtz decomposition and the fact $\delta(\mathbf{y}-\mathbf{x} ) = -\nabla^2 \, (4 \pi |\mathbf{y}-\mathbf{x}|)^{-1}$ tell us that

$$ \mathbf{v}(\mathbf{x})= \frac{c}{4 \pi} \int_\gamma ds \dfrac{ \mathbf{y}'(s) \times(\mathbf{x} - \mathbf{y}(s)) }{|\mathbf{x} - \mathbf{y}(s)|^3}$$

Again, the constant $c$ is just a physical constant that sets the value of the circulation of the field $\mathbf{v}$ around the vortex.

This is very clear and works in $\mathbb{R}^3$. Imagine now that the wire (or the curve that parametrizes the irrotational vortex) is a curve in the three-dimensional torus $\mathbb{T}^3 = S^1 \times S^1 \times S^1$. How to obtain the equivalent of the Biot-Savart law?

NOTE: we are changing the base manifold from $\mathbb{R}^3$ to $\mathbb{T}^3 $ but the local differential relations should be unchanged (i.e. the definition of the vorticity 2-form as external derivative of the velocity 1-form, or the local form of Maxwell equations $dF = J$). The problem is that the Biot-Savart law is non-local, so it is a global problem that "feels" the topology of the manifold. Maybe in the end the question is related to how the Helmholtz decomposition works on a torus.

from Hot Weekly Questions - Mathematics Stack Exchange
Quillo

Just Equations is a California based project dedicated to advancing math-related policies that give students the quantitative tools they need to advance in college and beyond. The project hopes to achieve this through research and analysis, strategic communications, convening of … Continue reading →

from Blog on math blogs https://ift.tt/3g98Dnq
Vanessa Rivera-Quinones

In Wells's book 《differential analysis on complex manifolds》 page219, there is a statement:" any compact Kähler manifold $X$ with the property that dim$_\mathbb{C}H^{1,1}(X)=1$ is necessarily Hodge. This follow from the fact that multiplication by an appropriate constant will make the Kähler form on $X$ integral."
But I know by Kodaira's Embedding theorem, a compact Kähler manifold is projective if and only if the Kähler class $[\omega]\in H^2(X,\mathbb{Z})$, I don't see dim$_\mathbb{C}H^{1,1}(X)=1$ imply $[\omega]\in H^2(X,\mathbb{Z})$, the reason is that $H^2(X,\mathbb{Z})$ can be seen as integral lattice in the vector space $H^2(X,\mathbb{C})$, and 1-dimensional $H^{1,1}(X,\mathbb{C})$ can be seen as a 1-dimensional sub vector space of $H^2(X,\mathbb{C})$, the intersection of $H^2(X,\mathbb{Z})$ and $H^{1,1}(X,\mathbb{C})$ may probably be empty? so that the compact Kähler manifold $X$ with dim$_\mathbb{C}H^{1,1}(X)=1$ is not necessarily Hodge? Is that right?

from Hot Weekly Questions - Mathematics Stack Exchange
Tom

Denote the unit ball for the $p$-norm in $\mathbb{R}^N$ with $p \in (0,1]$, $$S_p^N = \Big \{ x \in \mathbb{R}^N,\ \Big(\sum \limits_{i=1}^N |x_i|^p\Big)^{1/p} \le 1 \Big\}$$

We want to find a convex subset of this ball having maximum Lebesgue measure.

My conjecture is that this set is the biggest ball for the $1$-norm that fits inside $S_p^N$. Solving $\lambda S_1^N \subset S_p^N$ yields $\lambda \le N^{1-1/p}$. The points of intersection of $S_p^N$ and $N^{1-1/p}S_1^N$ are the all the points $\big(\pm N^{-1/p},...,\pm N^{-1/p}\big)$. The Lebesgue measure of this convex set is $\frac{2^N}{N!}N^{N\big(1-\frac{1}{p}\big)}$. Is that the highest volume of a convex set inside $S_p^N$?

$\hspace{7cm}$

For example, in $\mathbb{R}^2$, we have the figure just above. I can prove that among all losanges inside $S_{0.5}^2$, $\frac{1}{2}S_1^2$ has the highest volume, yet I can not prove that there are no other convex set that could be better, and I can't either generalize to higher dimensions.

from Hot Weekly Questions - Mathematics Stack Exchange
charmd

Let $E$ be a $\mathbb R$-Banach space, $x,y\in E$ and $\gamma\in C^1([0,1],E)$. Can we show that $$\int_0^1\left\|\gamma'(t)\right\|_E\:{\rm d}t\ge\left\|x-y\right\|_E?\tag1$$ Clearly, by the mean value inequality, there is a $t_0\in(0,1)$ with $\left\|\gamma'(t_0)\right\|_E\ge\left\|x-y\right\|_E$, but that doesn't seem to be helpful.

Intuitively, interpreting the left-hand side of $(1)$ at the length of the curve $\gamma$, it is clear that there is no shorter curve then a straight line ...

from Hot Weekly Questions - Mathematics Stack Exchange
0xbadf00d

I am trying to prove this. I used the telescoping method, but the problem is I need the first fraction to be $\frac{1}{4(n+1)}$ and I also tried to relate it to alternating Harmonic series which didn't work. Any hint would be greatly appreciated.$$\sum_{n=1}^{\infty}\left ( \frac{1}{4n+1}-\frac{1}{4n} \right )=\frac{1}{8}\left ( \pi-8+6\ln{2} \right )$$

from Hot Weekly Questions - Mathematics Stack Exchange
mike

submitted by /u/abhiachoudhary
[link] [comments]

from math https://ift.tt/2BjwIJi https://ift.tt/eA8V8J

submitted by /u/AutoModerator
[link] [comments]

from math https://ift.tt/2NEsXAP https://ift.tt/eA8V8J

     The categorization of different points of view as opposites can disappear as a unified system embraces both of them.  In mathematics, the counting numbers and their opposites become the integers,the rational and irrational numbers join to give the reals, the real and imaginary numbers yield the complex numbers.  In our global world with its biases and dangers and uncertainties, we will, I hope, evaluate our differences and unite our strengths to form a larger, stronger unity.
     A syllable-square poem by Carmela Martino (offered below) illustrates one of the unifications that can benefit our society: inclusion of the arts to enrich the sciences, from STEM forming STEAM.

Carmela Martino's poem first appeared here at TeachingAuthors.

from Intersections -- Poetry with Mathematics
https://ift.tt/2NKW0Tb
noreply@blogger.com (JoAnne Growney)

I am trying to find the result for the sum of the form

$\sum_{n=0}^{\infty}a^nq^{n^2}$.

The special case for $a=1$ is easily given by $\vartheta(0,q)$, where $\vartheta(z,q)$ is the third Jacobi Theta function. So, whatever the answer is, it must collapse to $\vartheta(0,q)$ for $a=1$.

I tried the approach:

$\sum_{n=0}^{\infty}\exp(2niz)q^{n^2}$, where $z=-i\frac{\ln(a)}{2}$, to make the summation look like $\vartheta(z,q)$. However, Jacobi Theta functions include summation from $-\infty$ to $\infty$, while I need it to start at 0.

I tried to use the Parseval's relation as well as several other methods but I cannot proceed any further.

Thank you.

from Hot Weekly Questions - Mathematics Stack Exchange
C.Koca

Differentiation of implicit functions. Hello friends, today I will talk about the differentiation of implicit functions. Have a look. If you’re looking for more in the differentiation of functions, do check out: Differentiation of parametric functions Differentiation of logarithmic functions How to differentiate inverse trigonometric functions Want to know more about the different rules in […]

The post Differentiation of implicit functions appeared first on Engineering Mathematics Tutorial.

from Engineering Mathematics Tutorial https://ift.tt/2ZdX6fK

Professional conferences often feature poster sessions, and, more often than not, the poster is simply incomprehensible to somebody walking through the aisles. So I enjoyed this article about an innovative way to bring scientific posters in the 21st century. The money quote: “The current method is not effective in communicating research findings. For instance, in […]

from Mean Green Math
John Quintanilla

I'm wondering whether there exists a geometric analog concept of absolute value. In other words, if absolute value can be defined as

$$ \text{abs}(x) =\max(x,-x) $$

intuitively the additive distance from $0$ to $x$, is there a geometric version

$$ \text{Geoabs}(x) = \max(x, 1/x) $$

which is intuitively the multiplicative "distance" from $1$ to $x$?

Update: Agreed it only makes sense for $Geoabs()$ to be restricted to positive reals.

To give some context on application, I am working on the solution of an optimization problem something like:

$$ \begin{array}{ll} \text{minimize} & \prod_i Geoabs(x_i) \\ \text{subject to} & \prod_{i \in S_j} x_i = C_j && \forall j \\ &x_i > 0 && \forall i . \end{array} $$

Basically want to satisfy all these product equations $j$ by moving $x_i$'s as little as possible from $1$. Note by the construction there are always infinite feasible solutions.

from Hot Weekly Questions - Mathematics Stack Exchange
dashnick

This question is kind of an extension of a previous question I asked here.

The infinite series $$\sum\frac{\mathrm{sgn}(\sin(n))}{n}$$ does converge, but I would like to know if Dirichlet's test can be used to prove the convergence with $$b_n=\mathrm{sgn}(\sin(n)).$$ So the question is, is the series $$B_n:=\sum_{k=1}^n\mathrm{sgn}(\sin(k))$$ unbounded? Loosely speaking it is a sum of $1$'s and the sign changes every $\pi$ terms. Also it would be great to know if the series is unbounded for other (irrational) changing cycles.

from Hot Weekly Questions - Mathematics Stack Exchange
Jaeseop Ahn

I was going through CMI 2019 paper, I stumbled upon the statement:

For $f:R\rightarrow R$, There are infinitely many continuous functions f for which $\int_0^1f(x)(1-f(x))dx=\frac{1}{4}$

My approach is, we can write $f(x)(1-f(x))=\frac{1}{4}-(f(x)-\frac{1}{2})^2$

Now, we can write $\int_0^1f(x)(1-f(x))dx=\frac{1}{4}-\int_0^1(f(x)-\frac{1}{2})^2dx$

$\Rightarrow \int_0^1(f(x)-\frac{1}{2})^2dx=0 \Rightarrow f(x)=\frac{1}{2}$

So, there must be only one function satisfying the condition. However, the official answer says the statement is true. Am I missing something?

from Hot Weekly Questions - Mathematics Stack Exchange
Mathsmerizing

submitted by /u/polyic
[link] [comments]

from math https://ift.tt/386aSFl https://ift.tt/eA8V8J

The answer is no for familiar operations of addition and multiplication. But could there exist any other operation that could turn the set of all negative real numbers into an abelian group. If yes, what is it? If no, how could I prove it?

from Hot Weekly Questions - Mathematics Stack Exchange
Yusuf

submitted by /u/Andy_Reds
[link] [comments]

from math https://ift.tt/2ZfzHup https://ift.tt/eA8V8J

submitted by /u/alphos74
[link] [comments]

from math https://ift.tt/3g4cja0 https://ift.tt/eA8V8J

Flag of the United States from 1777 to 1795.

In honor of Independence Day we thought it would be fun to look at one story about the first American Flag.

The rough design of the flag was drawn by a committee of George Washington, Robert Morris, and George Ross in 1776.  When approached by the committee, George Ross's niece, a respected seamstress, Betsy Ross, suggested some important changes.  One change was to use a 5-pointed star to represent each of the 13 colonies. The committee objected that a pentagram would be too hard to make. Betsy demonstrated that she could create the desired star by simply folding fabric and making just one scissors cut.  So, the design was changed.

How did she do that fold and cut?

The activity: BetsyRossStar.pdf

CCSS: 7.G.B, 8.G, HSG.CO

For members we have an editable Word docx and one solution to the folded line task.

BetsyRossStar.docx       FoldLines-solution.pdf

---

We also have two previous activities for the Fourth of July.

Fireworks on your calculator! Students experiment with their graphing calculators to create a fireworks display?  They manipulate parabolas and adjust their calculator windows.  We have a brief activity with task questions. CCSS:  HSA.SSE, HSF.IF

Flag Art A little ratio art might be a fun way to get ready for the Fourth of July. In this activity students measure; create whole number ratios for the official U.S. flag; decide how our artistic flags will be different from the official flag; make stars from regular pentagons, and finally create their own flag design. CCSS: 4.NBT, 4.NFB, 5.NBT, 5.NF.B, 6.RP.1, 6.RP.2, 6.RP.3, 7.RP.1, 7.RP.2, 7.G.1

from Yummy Math
Leslie

submitted by /u/xier_zhanmusi
[link] [comments]

from math https://ift.tt/2Vmn8vZ https://ift.tt/eA8V8J

Let $\mathcal{C}^0 ( [0, 1], \mathbb{R})$ denote the set of continuous functions from $[0, 1]$ to $\mathbb{R}$ and $\mathcal{C}^1 ( [0, 1], \mathbb{R})$ denote the set of class $\mathcal{C}^1$ functions from $[0, 1]$ to $\mathbb{R}$, both of these sets are algebras over the field $\mathbb{R}$.
The question is whether we can find an isomorphism of algebras:
$\Phi:\mathcal{C}^0 ( [0, 1], \mathbb{R})\longrightarrow\mathcal{C}^1 ( [0, 1], \mathbb{R})$
it seems, well at least to me, that such a cheesy isomorphism cannot exist, however I couldn't prove it.
I tried the obvious choice, which is proof by contradiction, and tried taking the inverse of such a function which would map differentiable functions to continuous ones, considering that one set already contains the other, however no contradiction seemed to arise.

from Hot Weekly Questions - Mathematics Stack Exchange
Lazarus

submitted by /u/AMA_About_Rampart
[link] [comments]

from math https://ift.tt/3dEmZdK https://ift.tt/eA8V8J

Prove or disprove:

There is a sequence $x$ with each $x_i\in\{1,2,3,4\}$ and $\pi$ can be written as the average $$\pi = \lim_{n\rightarrow\infty}\sum_{i=1}^{n}\frac{x_i}{n}$$

I am sure that this question would be trivial using advanced number theory concepts, but I would like a solution using just high-school olympiad level mathematics.

Thanks a lot. ☺

from Hot Weekly Questions - Mathematics Stack Exchange
N-N

submitted by /u/quark1415
[link] [comments]

from math https://ift.tt/2Vqy8J0 https://ift.tt/eA8V8J

submitted by /u/ItsYabboi
[link] [comments]

from math https://ift.tt/3eEjpBD https://ift.tt/eA8V8J

Let $a,b$ be two positive, nonsquare integers such that $a>b$. What is the smallest number $\kappa$ such that $$\left\{(a,b):a\sqrt b+b\sqrt a\,\,\text{is within}\,\,\frac1{(ab)^\kappa}\,\,\text{of an integer}\right\}$$ has finite cardinality?

Note that if $x$ has irrationality measure $\mu$ then $\mu$ is the smallest number (more precisely the infimum) such that $$0<\left|x-\frac pq\right|<\frac1{q^\mu}$$ has finitely many solutions for $p,q$ integers. Here, the problem can be rephrased as determining the smallest number $\kappa$ such that, $$0<\left|a\sqrt b+b\sqrt a-K\right|<\frac1{(ab)^\kappa}$$ has finitely many solutions for an integer $K(a,b)$ which is either $\lfloor a\sqrt b+b\sqrt a\rfloor$ or $\lceil a\sqrt b+b\sqrt a\rceil$. This formulation is close to the definition of an irrationality measure (which is $2$ in this case), but is not directly related since the parameters $p,q$ cannot be matched.

From empirical results, I believe that $\kappa\in(1,2)$, as letting $\kappa=2$ yielded no solutions for a long time. The code in PARI/GP is

squar(k)=for(a=2,+oo,for(b=2,a-1,if((issquare(a)==0 && frac(a*sqrt(b)+b*sqrt(a))<1/((a*b)^k)) || 1-frac(a*sqrt(b)+b*sqrt(a))<1/((a*b)^k),print1([a,b]," "))))

While I recognise that the question posed at the beginning of this post is extremely difficult to determine exactly, I would appreciate proofs that $\kappa>1$ or $\kappa<2$ should they be true.

_{Interestingly, when $a=b$, I haven't managed to find any solutions when $\kappa=1$. In fact, in this case, I conjecture that $\kappa\in(1/2,1)$.}

from Hot Weekly Questions - Mathematics Stack Exchange
TheSimpliFire

Yesterday, Peter Sarnak gave the London Mathematical Society’s 2020 Hardy Lecture (remotely). He talked about gaps in the spectra of connected cubic graphs. It was a talk properly described as a tour de force, applying to the problem ideas from algebraic geometry (Weil’s proof of the Riemann conjecture for curves over finite fields), probability (Benjamini–Schramm measure), and fractal geometry (the Julia set of a real quadratic), among many other things.

I won’t attempt to describe more than the first few ideas in the talk. I think it was filmed, and a video will no doubt appear at some point; I do urge you to watch it.

Let X be the set of all finite connected cubic graphs (graphs of valency 3). We are interested in spectral questions; the spectrum of a member of X is the set (or multiset) of eigenvalues of its adjacency matrix. Since the graphs are regular, the adjacency spectrum is a simple transform of the Laplacian spectrum. It is well known that the eigenvalues of such a graph are all real, and lie in the interval [−3,3]; the value 3 is always a simple eigenvalue, and −3 is an eigenvalue if and only if the graph is bipartite.

A subinterval I of [−3,3] is a gap if there exist arbitrarily large graphs in X with no eigenvalues in this interval; it is maximal if there is no strictly larger interval which is a gap.

The first gap is (2√2,3), due to Alon and Boppana; the maximality of this gap depends on the existence of Ramanujan graphs, shown in the 1980s by Margulis and by Lubotzky, Phillips and Sarnak. As the name suggests, the construction of such graphs uses a substantial amount of number theory related to work of Ramanujan. The speaker told us that he had been rash enough to state that the construction would not be possible without number theory; but he was proved wrong (and taught to be more cautious) when a group of physicists found a construction using Lee–Yang theory in statistical mechanics.

I was so impressed with the Lubotzky–Phillips–Sarnak paper when it came out that I gave a seminar talk to the pure mathematicians at Queen Mary expounding it.

Then Peter Sarnak mentioned two other potential gaps, interest in which had come from real applications: gaps at −3, important in the theory of waveguides; and gaps at 0, important in the Hückel theory of fullerenes (molecules made of carbon atoms forming polyhedra with only pentagonal and hexagonal faces, like the football (which chemists call the buckyball). I will just repeat some of what he said about the first of these two.

He and Alicia Kollár (and others) have shown the remarkable result that [−3,−2) is a maximal gap. He associates the name of Alan Hoffman with this gap. The name is entirely appropriate. Hoffman did a lot of work on graphs with least eigenvalue −2, but in the end it was Jean-Marie Goethals, Jaap Seidel, Ernie Shult and I who proved the theorem he had been trying to prove, giving a virtually complete description of such graphs. I have described our result here; Peter Sarnak was kind enough to describe the paper as “beautiful”, and I don’t mind shining in reflected glory for a moment.

So here is the path from our theorem to the gap described above; the details were not given in the lecture.

We showed that, with finitely many exceptions (all realised in the exceptional root system E₈), all connected graphs with smallest eigenvalue −2 (or greater) are what Hoffman called generalised line graphs. Fortunately I don’t have to tell you what these are, since it is an easy exercise to show that if a generalised line graph is regular, then it is either a line graph or a cocktail party (n couples attend a cocktail party, and each person talks to everyone except his/her partner). Moreover, if a line graph is regular, then it is the line graph of either a regular graph or a semiregular bipartite graph.

The cocktail party graph has valency 2n−2, which is even; so is not possible in our situation. The line graph of a regular graph of valency k has valency 2k−2, which is also even. The line graph of a semiregular bipartite graph with valencies k and l has valency k+l−2. So in our situation we only have to consider line graphs of semiregular bipartite graphs where the valencies in the two bipartite blocks are 2 and 3.

Now such a graph is obtained from a smaller graph Y in X (namely, the induced subgraph of the distance-2 graph on the set of vertices of valency 3) by inserting a vertex in each edge. So its line graph is built from Y by replacing each vertex of Y by a triangle, or sewing in triangles.

We conclude that, with finitely many exceptions, any graph in X with no eigenvalues in [−3,−2) is obtained from a graph in X by sewing in triangles. Moreover, such graphs are line graphs of graphs with more edges than vertices, and so really do have −2 as an eigenvalue; so the gap is maximal.

from Peter Cameron's Blog https://ift.tt/38b7jNZ
Peter Cameron

submitted by /u/ItsYabboi
[link] [comments]

from math https://ift.tt/2YCPS5I https://ift.tt/eA8V8J

Let $f:I \longrightarrow \mathbb{R}$ be differentiable in a inner point $\xi \in I$.

Show that $$\lim\limits_{h \rightarrow 0}\frac{f(\xi+h)-f(\xi-h)}{2h}$$

exists and is $f'(\xi)$.

Also give an example which shows, that the existence of this limit, doesnt mean, that $f$ is necessary differentiable in $\xi$.

---

My attempt:

Given is that:

$$\lim\limits_{h\rightarrow0}\frac{f(\xi+h)-f(\xi)}{h}=f'(\xi)$$

exists.

If $\,\lim\limits_{h \rightarrow 0}\frac{f(\xi+h)-f(\xi-h)}{2h}=\lim\limits_{h\rightarrow0}\frac{f(\xi+h)-f(\xi)}{h}=f'(\xi)$ then:

$$\lim\limits_{h\rightarrow0}\left(\frac{f(\xi+h)-f(\xi)}{h}-\frac{f(\xi+h)-f(\xi-h)}{2h}\right)=0$$

$$\lim\limits_{h\rightarrow0}\frac{2(f(\xi+h)-f(\xi))-f(\xi+h)+f(\xi-h)}{2h}=\lim\limits_{h\rightarrow0}\frac{f(\xi+h)-f(\xi)+f(\xi-h)-f(\xi)}{2h}=0$$

$$=\frac{1}{2}\lim\limits_{h\rightarrow0}\frac{f(\xi+h)-f(\xi)}{h}+\frac{1}{2}\lim\limits_{h\rightarrow0}\frac{f(\xi-h)-f(\xi)}{h}=\frac{1}{2}\lim\limits_{h\rightarrow0}\frac{f(\xi+h)-f(\xi)}{h}-\frac{1}{2}\lim\limits_{h\rightarrow0}\frac{f(\xi)-f(\xi-h)}{h}=\frac{1}{2}f'(\xi)-\frac{1}{2}f'(\xi)=0$$

$\Box$

Let $f:\mathbb{R}\longrightarrow \mathbb{R}:x \mapsto |x|$

Then for $\xi=0$:

$$\lim\limits_{h \rightarrow 0}\frac{f(\xi+h)-f(\xi-h)}{2h}=\lim\limits_{h \rightarrow 0}\frac{|h|-|-h|}{2h}=\lim\limits_{h \rightarrow 0}\frac{|h|-|h|}{2h}=\lim\limits_{h \rightarrow 0}0=0$$

$\Longrightarrow$ the limit exists, but $f$ is not differentiatable at $\xi=0$

---

Hello, as always it would help me alot, if someone could look over it and give me feedback weither my work is correct. And if not, what is wrong :) thank you

from Hot Weekly Questions - Mathematics Stack Exchange
CoffeeArabica

This may be a stupid question to some, but when i calculate a cross product of two vectors. For example the first coordinate of the solution. I put my finger on the first line, then i calculate something that seems like the determinant of a 2x2 matrix.

Is there any connection between matrices and the cross product?

Sorry if that is a stupid qustion, but I am in the second semester and haven't found an answer in the internet.

Thank you for your help!

from Hot Weekly Questions - Mathematics Stack Exchange
David Reiter

submitted by /u/NuBoston
[link] [comments]

from math https://ift.tt/3i773Eo https://ift.tt/eA8V8J

An infinitely long wire carries a constant electric current $I$ along the $z$ axis. Thus, the current density $\mathbf{j}$ of the wire is given by, in cartesian coordinates:

$$\mathbf{j}(\mathbf{r})=I\delta(x)\delta(y)\mathbf{\hat{z}}$$

I am required to calculate the following integral:

$$\mathcal{I}=\iint_S\mathbf{j}(\mathbf{r})\cdot\mathbf{\hat{z}}\ \text{d}S$$

Where $S$ is a circle with radius $R>0$ on the $[XY]$ plane. Calculating $\mathcal{I}$ in cartesian coordinates gives:

$$\mathcal{I}_{\text{cartesian}}=I\int_{-R}^{+R}\int_{-\sqrt{R^2-x^2}}^{+\sqrt{R^2-x^2}}\delta(x)\delta(y)\ \text{d}y\text{d}x\underbrace{=}_{0\in(-\sqrt{R^2-x^2},+\sqrt{R^2-x^2})}I\int_{-R}^{+R}\delta(x)\ \text{d}x\underbrace{=}_{0\in[-R,+R]}I$$

However, when I try to calculate the integral using polar coordinates, where:

$$\delta(x)\delta(y)=\frac{\delta(r)}{2\pi r}$$

I get:

$$\mathcal{I}_{\text{polar}}=I\int_{0}^{2\pi}\int_{0}^{R}\frac{\delta(r)}{2\pi r}\ r\text{d}r\text{d}\theta=I\int_0^R\delta(r)\ \text{d}r$$

Because of course $\mathcal{I}_{\text{cartesian}}=\mathcal{I}_{\text{polar}}$, the integral I got should be equal to $1$, but I don't understand why. From my personal experience, integrals like this, where the zero of the argument of the dirac-delta function is one of the integral limits, are not well-defined. Why then in this case it is equal to $1$? I suspect my construction of the integral is wrong, but I'm not sure where I was wrong.

Thanks!

from Hot Weekly Questions - Mathematics Stack Exchange
Amit Zach

My STEP students invented a coin-flipping game that doesn’t require a coin. It is called The No-Flippancy Game.

Alice and Bob choose distinct strings of length n consisting of the letters H (for heads) and T (for tails). The two players alternate selecting the outcome of the next “flip” to add to the sequence by the rule below.

The “flip” rule: Let i < n be the maximal length of a suffix of the sequence of chosen outcomes that coincides with a prefix of the current player’s string. The player then selects the element of their string with index i + 1 as the next term in the sequence.

Alice goes first, and whoever’s string appears first in the sequence of choices wins. In layman terms, the game rules mean that the players are not strategizing, but rather greedily finishing their strings.

Suppose n = 2 and Alice chose HH. If Bob chooses HT, then Bob wins. Alice has to choose H for the first flip. Then Bob chooses T and wins. On the other hand, if Bob chooses TT for his string, the game becomes infinite. On her turn Alice always chooses H, while on his turn Bob always chooses T. The game outcome is an alternating string HTHTHT… and no one wins.

Suppose n = 4, Alice chooses HHTT, and Bob chooses THHH. The game proceeds as HTHHTHHH, at which point Bob wins.

This game is very interesting. The outcome depends on how Alice’s and Bob’s chosen strings overlap with each other. We wrote a paper about this game, which is available at math.CO arXiv:2006.09588.

Share:

from Tanya Khovanova's Math Blog https://ift.tt/2ZfxCP0
tanyakh